Résolution dans N3

[horido]

Bonjour,

je cherche à résoudre le problème suivant: de combien de façons différents peut-on payer 100 euros avec des pièces de 10ct, 20ct, et 50 ct?
J'ai posé: x+2y+5z= 1000.
Quelqu'un peut-il me donner une piste pour la suite?

[capitaine nuggets]

Bonjour,

je cherche à résoudre le problème suivant: de combien de façons différents peut-on payer 100 euros avec des pièces de 10ct, 20ct, et 50 ct?
J'ai posé: x+2y+5z= 1000.
Quelqu'un peut-il me donner une piste pour la suite?

100 ou 1000 euros ?
Il suffit de chercher toutes les manières différentes de payer 1 euro uniquement avec des pièces de 10,20 et 50 centimes (pourquoi ?).
Du coup, le problème se simplifie un peu :+++:

[chan79]

un petit programme donne le résultat en 1 seconde (algobox suffit)

[horido]

100 ou 1000 euros ?
Il suffit de chercher toutes les manières différentes de payer 1 euro uniquement avec des pièces de 10,20 et 50 centimes (pourquoi ?).
Du coup, le problème se simplifie un peu :+++:

C'est 100 euros en fait. J'ai trouvé ce problème sur internet et le résultat est 50401.Mais je n'arrive pas à parvenir à cette solution. Voici un lien:

http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=9&cad=rja&uact=8&ved=0CFMQFjAI&url=http%3A%2F%2Fexo7.emath.fr%2Fficpdf%2Ffic00095.pdf&ei=NjKgVLGfJYrkasz4grgP&usg=AFQjCNFNFdp7bX6QmPdQUOF5CyPRcYlnMg&bvm=bv.82001339,d.d2s

Je ne comprend pas leur méthode. Si quelqu'un peut m'en dire plus merci.

[chan79]

Dans un premier temps, ils dénombrent le nombre de solutions de x+2y=k (avec k entier naturel)
On peut écrire x=k-2y
il faut que x soit positif soit k-2y>=0 soit y<k/2
y doit être entier positif donc il y a autant de solutions que d'entiers compris entre 0 et E(k/2)

le nombre de solutions est 1+E(k/2)
Dans leur correction, ils ont mis k=0 au lieu de y=0 sous le premier signe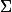

Sinon, avec un ordinateur, on fait deux boucles

[horido]

100 ou 1000 euros ?
Il suffit de chercher toutes les manières différentes de payer 1 euro uniquement avec des pièces de 10,20 et 50 centimes (pourquoi ?).
Du coup, le problème se simplifie un peu :+++:

J'ai trouvé 9 façons de payer 1 euro.

[horido]

Dans un premier temps, ils dénombrent le nombre de solutions de x+2y=k (avec k entier naturel)
On peut écrire x=k-2y
il faut que x soit positif soit k-2y>=0 soit y<k/2
y doit être entier positif donc il y a autant de solutions que d'entiers compris entre 0 et E(k/2)

le nombre de solutions est 1+E(k/2)
Dans leur correction, ils ont mis k=0 au lieu de y=0 sous le premier signe

Sinon, avec un ordinateur, on fait deux boucles

Merci pour ton explication.J'ai trouvé 9 façons de payer 1 euro.C'est une bonne simplification.Je vais chercher la suite.

[chan79]

Merci pour ton explication.J'ai trouvé 9 façons de payer 1 euro.C'est une bonne simplification.Je vais chercher la suite.

Tu as dû en oublier un.
(10,0,0) puisque 10*0.10+0*0.20+0*0.50=1
(5,0,1)
(0,0,2)
(8,1,0)
(3,1,1)
(6,2,0)
(1,2,1)
(4,3,0)
(2,4,0)
(0,5,0)

[horido]

Tu as dû en oublier un.
(10,0,0) puisque 10*0.10+0*0.20+0*0.50=1
(5,0,1)
(0,0,2)
(8,1,0)
(3,1,1)
(6,2,0)
(1,2,1)
(4,3,0)
(2,4,0)
(0,5,0)

oui j'ai oublié(0,0,2).Et pour 2 euros combien obtient-on de combinaisons?

[horido]

J'ai trouvé 9 façons de payer 1 euro.

Correction: il y a 10 façons de payer 1 euros;

[horido]

Tu as dû en oublier un.
(10,0,0) puisque 10*0.10+0*0.20+0*0.50=1
(5,0,1)
(0,0,2)
(8,1,0)
(3,1,1)
(6,2,0)
(1,2,1)
(4,3,0)
(2,4,0)
(0,5,0)

J'ai trouvé. J'ai dénombré le nombre de solutions en commençant par z=0 jusqu'à z=200.Et en ajoutant les solutions on fait la somme de 2 suites arithmétiques.