Bonjour,
J'ai un problème sur le calcul d' une variance
V (x;) ) = V( (;)xi) / 10 ) = (1/10^2) * 10 * V (x) tel que i soit compris entre 1 et 10 compris et x;) (x barre) est la moyenne des xi dans l'échantillon de 10 individus, je ne comprends pas j'aurai mis 10^2 au lieu de 10 ????
merci :mur:
Variance de variables aléatoires
5 messages
- Page 1 sur 1
margotv a écrit:Bonjour,
J'ai un problème sur le calcul d' une variance
V (x;) ) = V( (;)xi) / 10 ) = (1/10^2) * 10 * V (x) tel que i soit compris entre 1 et 10 compris et x;) (x barre) est la moyenne des xi dans l'échantillon de 10 individus, je ne comprends pas j'aurai mis 10^2 au lieu de 10 ????
merci :mur:
C'est possible ça, de calculer la variance de la moyenne ? On calcule la variance d'une série, pas d'un nombre. Étrange.
En fait l' énoncé est :
dans une population, on suppose qu'un paramètre biologique P (mesuré dans une unité u) est modélisé par une variable continue distribuée selon une loi normale N de variance ;)^2 et d'espérance (ou moyenne) 70 u. on étudie un échantillon de 10 individus issus de cette population. sur chacun d'entre eux on a réalisé un dosage de paramètre. le dosage de paramètre biologique P pour le i eme individu de l'échantillon est représenté par Xi. Les variables Xi (i compris entre 1 et 10 compris) sont indépendantes et identiquement distribuées selon la loi normale N. on note x;) (grand x barre) la moyenne des xi (grand xi) dans l'échantillon . calculer la variance de grand x
la réponse : V (x;) ) = V( (;)xi) / 10 ) = (1/10^2) * 10 * V (x) . je ne comprends pas j'aurai mis 10^2 au lieu de 10
MERCI :)
dans une population, on suppose qu'un paramètre biologique P (mesuré dans une unité u) est modélisé par une variable continue distribuée selon une loi normale N de variance ;)^2 et d'espérance (ou moyenne) 70 u. on étudie un échantillon de 10 individus issus de cette population. sur chacun d'entre eux on a réalisé un dosage de paramètre. le dosage de paramètre biologique P pour le i eme individu de l'échantillon est représenté par Xi. Les variables Xi (i compris entre 1 et 10 compris) sont indépendantes et identiquement distribuées selon la loi normale N. on note x;) (grand x barre) la moyenne des xi (grand xi) dans l'échantillon . calculer la variance de grand x
la réponse : V (x;) ) = V( (;)xi) / 10 ) = (1/10^2) * 10 * V (x) . je ne comprends pas j'aurai mis 10^2 au lieu de 10
MERCI :)
Salut,
Si tu as ce type d'exo. a faire, j'aurais tendance a supposer qu tu as vu que la somme de deux normales indépendantes est une normale (d'espérance la somme des espérances et de variance la somme des variances).
Vu les hypothèses faites, ça te donne direct la loi de : c'est une normale d'espérance
: c'est une normale d'espérance  et de variance
et de variance  .
.
Comme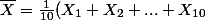) , il suit lui aussi une loi normale.
, il suit lui aussi une loi normale.
Son espérance est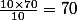 et sa variance
et sa variance 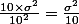
Si tu as ce type d'exo. a faire, j'aurais tendance a supposer qu tu as vu que la somme de deux normales indépendantes est une normale (d'espérance la somme des espérances et de variance la somme des variances).
Vu les hypothèses faites, ça te donne direct la loi de
Comme
Son espérance est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
