Jordanisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Déc 2014, 15:15
par capitaine nuggets » 18 Déc 2014, 15:15
Bonjour, j'aurais besoin d'aide pour "jordaniser" une matrice, je ne me souviens plus trop de la méthode à effectuer...
Soit la matrice

(triangulaire supérieure par blocs donc :we: ).
J'ai donc commencé par calculer sont polynôme caractéristique
=(X+3)^4)
.
Donc
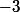
est l'unique valeur propre de multiplicité algébrique

.
Je sais donc que la matrice

semblable à une matrice

où a,b,c sont des éléments de
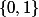
.
Mais je n'ai aucune idée de comment poursuivre la "jordanisation".
Merci d'avance pour votre aide :+++:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Déc 2014, 15:44
par capitaine nuggets » 18 Déc 2014, 15:44
Quelques calculs fastidieux si ça peux servir :
Soit
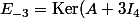)
le sous-espace propre associé à la valeur propre -3.
J'ai trouvé que :
-
=2)
;
-
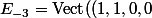,(-4,0,2,1)))
.
***************************************************************************
Soit
}= {\rm Ker}\left( (A+3I_4)^2 \right))
.
J'ai trouvé que :
-
^2 = \begin{pmatrix} 0 & 0 & -4 & 8 \\ 0 & 0 & -4 & 8 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})
;
-
})=3)
;
-
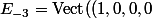,(0,1,0,0),(0,0,2,1)))
.
***************************************************************************
Soit
}= {\rm Ker}\left( (A+3I_4)^3 \right))
.
J'ai trouvé que :
-
^3 = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})
;
-
})=4)
;
-
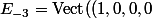,(0,1,0,0),(0,0,1,0),(0,0,0,1)))
.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Déc 2014, 21:14
par capitaine nuggets » 18 Déc 2014, 21:14
Quelques calculs fastidieux si ça peux servir :Soit
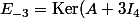)
le sous-espace propre associé à la valeur propre -3.
J'ai trouvé que :
-
=2)
;
-
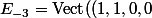,(-4,0,2,1)))
.
***************************************************************************
Soit
}= {\rm Ker}\left( (A+3I_4)^2 \right))
.
J'ai trouvé que :
-
^2 = \begin{pmatrix} 0 & 0 & -4 & 8 \\ 0 & 0 & -4 & 8 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})
;
-
})=3)
;
-
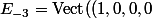,(0,1,0,0),(0,0,2,1)))
.
***************************************************************************
Soit
}= {\rm Ker}\left( (A+3I_4)^3 \right))
.
J'ai trouvé que :
-
^3 = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})
;
-
})=4)
;
-
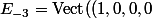,(0,1,0,0),(0,0,1,0),(0,0,0,1)))
.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2014, 21:42
par Ben314 » 18 Déc 2014, 21:42
Salut,
C'est effectivement ça qu'il faut faire comme calculs.
Après, tu part d'un vecteur quelconque

de E qui
n'est pas dans
^2))
: dans ta base, tu peut déjà mettre

,
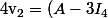(v_1))
,
^2(v_1))
qui forment forcément une famille libre (pourquoi ?)
Et ça te donne déjà 3 des vecteurs ainsi qu'une grande partie de la matrice que tu cherche.
Après, il te manque un vecteur. Oukilé ? (et pourquoi kilélà ?)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 19 Déc 2014, 17:31
par capitaine nuggets » 19 Déc 2014, 17:31
Ben314 a écrit:Salut,
C'est effectivement ça qu'il faut faire comme calculs.
Après, tu part d'un vecteur quelconque

de E qui
n'est pas dans
^2))
: dans ta base, tu peut déjà mettre

,
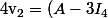(v_1))
,
^2(v_1))
qui forment forcément une famille libre (pourquoi ?)
Et ça te donne déjà 3 des vecteurs ainsi qu'une grande partie de la matrice que tu cherche.
Après, il te manque un vecteur. Oukilé ? (et pourquoi kilélà ?)
:hum: Je n'arrive pas à répondre à tes questions. Pourrais-tu m'aiguiller un peu plus stp ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2014, 18:46
par Ben314 » 19 Déc 2014, 18:46
Si tu suppose que

et que tu applique
^2)
ainsi que

a cette égalité, ça te donne quoi ?
(ne pas oublier que

est dans
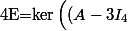^3\big))
mais n'est pas dans
^2\big))
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 20 Déc 2014, 09:15
par capitaine nuggets » 20 Déc 2014, 09:15
Ben314 a écrit:Salut,
C'est effectivement ça qu'il faut faire comme calculs.
Après, tu part d'un vecteur quelconque

de E qui
n'est pas dans
^2))
: dans ta base, tu peut déjà mettre

,
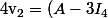(v_1))
,
^2(v_1))
qui forment forcément une famille libre (pourquoi ?)
Et ça te donne déjà 3 des vecteurs ainsi qu'une grande partie de la matrice que tu cherche.
Après, il te manque un vecteur. Oukilé ? (et pourquoi kilélà ?)
Ben314 a écrit:Si tu suppose que

et que tu applique
^2)
ainsi que

a cette égalité, ça te donne quoi ?
(ne pas oublier que

est dans
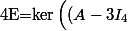^3\big))
mais n'est pas dans
^2\big))
.
Voici ce que j'obtiens :
(\alpha_1 v_1+\alpha_2 v_2+\alpha_3 v_3)=0_E)
( v_1)+\alpha_2 (A-3I_4)( v_2)+\alpha_3 (A-3I_4)( v_3)=0_E)
( v_1)+\alpha_2 (A-3I_4)^2( v_1)+\alpha_3 (A-3I_4)^3( v_1)=0_E)
ET
^2( v_1)+\alpha_2 (A-3I_4)^3( v_1)+\alpha_3 (A-3I_4)^4( v_1)=0_E)
D'ailleurs, pourquoi on manipule des puissances de
)
et pas de
)
?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Déc 2014, 09:59
par Ben314 » 20 Déc 2014, 09:59
capitaine nuggets a écrit:D'ailleurs, pourquoi on manipule des puissances de
)
et pas de
)
?
Parce que... je me suis gouré la première fois en recopiant ton A+3I puis que j'ai recopié ce A-3I (faux) tout le long des posts...

Donc c'est
absolument partout des A+3I...
Aprés, le truc couillon à voir, c'est que, vu que

est dans
^3))
mais pas dans
^2))
, ça implique que
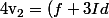(v_1))
est dans
^2))
mais pas dans
))
, et que
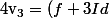(v_2))
est dans
)
mais n'est pas nul.
Donc dans tes 3 équations, il y a plein de trucs nuls.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 20 Déc 2014, 13:10
par capitaine nuggets » 20 Déc 2014, 13:10
capitaine nuggets a écrit:Voici ce que j'obtiens :
(\alpha_1 v_1+\alpha_2 v_2+\alpha_3 v_3)=0_E)
( v_1)+\alpha_2 (A-3I_4)( v_2)+\alpha_3 (A-3I_4)( v_3)=0_E)
( v_1)+\alpha_2 (A-3I_4)^2( v_1)+\alpha_3 (A-3I_4)^3( v_1)=0_E)
ET
^2( v_1)+\alpha_2 (A-3I_4)^3( v_1)+\alpha_3 (A-3I_4)^4( v_1)=0_E)
D'ailleurs, pourquoi on manipule des puissances de
)
et pas de
)
?
Ok, donc si je reprends, j'ai :
( v_1)+\alpha_2 (A+3I_4)^2( v_1)=0_E)
ET
^2( v_1)=0_E)
Mais quelle est l'idée derrière tout ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
de E qui n'est pas dans
: dans ta base, tu peut déjà mettre
,
,
qui forment forcément une famille libre (pourquoi ?)
de E qui n'est pas dans
: dans ta base, tu peut déjà mettre
,
,
qui forment forcément une famille libre (pourquoi ?)
et que tu applique
ainsi que
a cette égalité, ça te donne quoi ?
est dans
mais n'est pas dans
.
et pas de
?
et pas de
?