Polynômes: du mal à appréhender cela!!

[jlb]

Bonsoir, le truc, est que je viens de me rendre compte qu'il existe des polynômes par exemple de degré 1 avec plusieurs racines. Est-ce envisageable d'avoir un polynôme de degré fini avec une infinité de racines? Auriez-vous un exemple pas trop compliqué si cela existe?

(p_6(3)X + p_6(3) dans Z/6Z a pour racines p_6(1), p_6(5) et p_6(3) par exemple)

Merci.

[capitaine nuggets]

Bonsoir, le truc, est que je viens de me rendre compte qu'il existe des polynômes par exemple de degré 1 avec plusieurs racines. Est-ce envisageable d'avoir un polynôme de degré fini avec une infinité de racines? Auriez-vous un exemple pas trop compliqué si cela existe?

( 3X + 3 dans Z/6Z a pour racines p_6(1), p_6(5) et p_6(3) par exemple)

Merci.

J'ai pas bien compris ton exemple.

Sinon oui, on a le résultat suivant :
Si est un anneau intègre alors tout polynôme de de degré admet au plus racines dans .
Ce résultat est faux : si on choisit dans , alors est de degré et admet exactement racines dans , à savoir .

Alors après, un polynôme de degré fini avec une infinité de racines, à priori, je ne pense pas (à vérifier).
On a toujours le polynôme nul de degré qui admet une infinité de racines si est infini.

[jlb]

J'ai pas bien compris ton exemple.

Sinon oui, on a le résultat suivant :
Si est un anneau intègre alors tout polynôme de de degré admet au plus racines dans .
Ce résultat est faux : si on choisit dans , alors est de degré et admet exactement racines dans , à savoir .

Plutôt deux racines p_10(0) et p_10(5) sinon, oui, c'est le même style d'exemple que le mien.
Mais pour un anneau non fini, cela doit être envisageable de créer un polynôme de degré fini avec une infinité de racines ou bien un argument ne le permet pas?

[capitaine nuggets]

Plutôt deux racines p_10(0) et p_10(5) sinon, oui, c'est le même style d'exemple que le mien.
Mais pour un anneau non fini, cela doit être envisageable de créer un polynôme de degré fini avec une infinité de racines ou bien un argument ne le permet pas?

Oulah oui, dsl j'étais avec un autre truc :++:

[Ben314]

Salut,
Deux "contres exemples" à mon avis :
- Les quaternions qui est un corps (donc intègre) mais non commutatif dans lequel, par exemple, X²=-1 admet une infinité de racines.
- L'anneau des polynômes à coeff. dans Z/4Z (par exemple) est commutatif mais non intègre et l'équation 2X=0 admet une infinité de racines.

Par contre, dans un anneau intègre et commutatif, un polynôme de degré d admet au plus d racines.

[jlb]

Salut,
Deux "contres exemples" à mon avis :
- Les quaternions qui est un corps (donc intègre) mais non commutatif dans lequel, par exemple, X²=-1 admet une infinité de racines.
- L'anneau des polynômes à coeff. dans Z/4Z (par exemple) est commutatif mais non intègre et l'équation 2X=0 admet une infinité de racines.

Par contre, dans un anneau intègre et commutatif, un polynôme de degré d admet au plus d racines.

Bonjour et merci, je ne connais pas bien le corps des quaternions ( je pensais qu'il était composé par 8 éléments?)
On peut pour le deuxième exemple?? le coefficient 2 est la classe de 2 et comme racine, tu prends quoi pour que le produit classe de 2 fois... soit défini? J'aurai dit qu'il n'a que deux racines: la classe de 0 et celle de 2?

En réfléchissant aux quelques anneaux non finis que je connaissais, j'ai pensé à cela: on considère l'anneau des suites et la suite u définie par u0=1 et pour n différent de 0, u_n=0 alors le polynôme uX admet une infinité de racines: toute suite dont le premier terme est 0. Est-ce que cela fonctionne?

Anneau intègre commutatif, cela suffit comme condition?? tu aurais une référence pour ce résultat?
Merci encore.

[Ben314]

Le terme "quaternions" peut désigner deux choses (au moins...) :
- Le groupe des quaternions qui a effectivement 8 éléments en général notés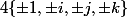 sur lequel on a une seule opération (la multiplication)
- Le corps des quaternions qui est l'ensemble des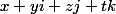 avec 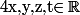sur lequel on a deux opération (addition et multiplication)
Ici, vu le contexte où on parle de polynômes, ce qui demande a avoir deux opérations (addition et multiplication), c'est forcément du deuxième qu'il s'agit et le corps en question est clairement infini vu qu'il s'agit d'un -e.v. de dim. 4 (on peut aussi plus simplement dire qu'il est infini vu qu'il contient )

Concernant l'autre exemple, il n'y a rien "à définir" : lorsqu'on dit "l'anneau Z/4Z", ça signifie que, sur cet ensemble là, les opérations sont celles contenues dans la définition générale de "l'anneau Z/nZ" que tu doit avoir dans ton cours.
Puis, lorsqu'on dit "l'anneau des polynômes à coeff. dans Z/4Z", ça signifie que, sur cet ensemble là, les opérations sont celles contenues dans la définition de "l'anneau A[X] des polynômes à coeff. dans l'anneau A" qui doit aussi être dans ton cours.

Concernant le "théorème" disant que, si A est commutatif et intègre alors tout polynôme de A[X] de degré d admet au plus d racines, cela résulte du fait que, si A est commutatif, si P(X) est dans A[X] et que xo est une racine de P(X) alors P(X)=(X-xo)Q(X) pour un certain Q de A[X]. Ensuite, vu que A est intègre, on a P(x)=0 ssi x=x0 ou bien Q(X)=0 et on conclue par récurrence.
Je ne connais pas de "nom" a ce résultat (en a-t-il un ?) ni de référence (vu que la preuve tient une ligne...)

[jlb]

Le terme "quaternions" peut désigner deux choses (au moins...) :
- Le groupe des quaternions qui a effectivement 8 éléments en général notés sur lequel on a une seule opération (la multiplication)
- Le corps des quaternions qui est l'ensemble des avec sur lequel on a deux opération (addition et multiplication)
Ici, vu le contexte où on parle de polynômes, ce qui demande a avoir deux opérations (addition et multiplication), c'est forcément du deuxième qu'il s'agit et le corps en question est clairement infini vu qu'il s'agit d'un -e.v. de dim. 4 (on peut aussi plus simplement dire qu'il est infini vu qu'il contient )

Concernant l'autre exemple, il n'y a rien "à définir" : lorsqu'on dit "l'anneau Z/4Z", ça signifie que, sur cet ensemble là, les opérations sont celles contenues dans la définition générale de "l'anneau Z/nZ" que tu doit avoir dans ton cours.
Puis, lorsqu'on dit "l'anneau des polynômes à coeff. dans Z/4Z", ça signifie que, sur cet ensemble là, les opérations sont celles contenues dans la définition de "l'anneau A[X] des polynômes à coeff. dans l'anneau A" qui doit aussi être dans ton cours.

Concernant le "théorème" disant que, si A est commutatif et intègre alors tout polynôme de A[X] de degré d admet au plus d racines, cela résulte du fait que, si A est commutatif, si P(X) est dans A[X] et que xo est une racine de P(X) alors P(X)=(X-xo)Q(X) pour un certain Q de A[X]. Ensuite, vu que A est intègre, on a P(x)=0 ssi x=x0 ou bien Q(X)=0 et on conclue par récurrence.
Je ne connais pas de "nom" a ce résultat (en a-t-il un ?) ni de référence (vu que la preuve tient une ligne...)

Merci pour ces réponses, je vais étudier cela. J'ai par contre une question: cela suffit A integre et commutatif pour factoriser par X-x0? Dans mon cours, on indique que A doit être un corps pour pouvoir justifier cette factorisation. En tout cas merci, pour tes explications.

[Ben314]

...si A est commutatif, si P(X) est dans A[X] et que xo est une racine de P(X) alors P(X)=(X-xo)Q(X) pour un certain Q de A[X].

Pas besoin ni d'intégrité, ni du fait que ce soit un corps pour avoir la factorisation :
Si xo est racine de P alors 0 est une racine du polynôme S(Y)=P(Y+xo) donc le terme constant de S est nul ce qui signifie que S(Y)=Y.T(Y) pour un certain polynôme T de A[X] et on donc P(X)=S(X-xo)=(X-xo).T(X-Xo)=(X-xo).Q(X)

[jlb]

Pas besoin ni d'intégrité, ni du fait que ce soit un corps pour avoir la factorisation :
Si xo est racine de P alors 0 est une racine du polynôme S(Y)=P(Y+xo) donc le terme constant de S est nul ce qui signifie que S(Y)=Y.T(Y) pour un certain polynôme T de A[X] et on donc P(X)=S(X-xo)=(X-xo).T(X-Xo)=(X-xo).Q(X)

Merci beaucoup.