soit E un espace vectoriel de dimension n
soit u un endomorphisme de E
alors on a E=Ker(u^n)Im(u^n)
qu'est ce que vous pensez sur ce resultat?
Somme directe
6 messages
- Page 1 sur 1
C'est très intéressant :we: mais il faut le démontrer. Il suffit de montrer que l'intersection des deux sous-espaces est  . Raisone par l'absurde, si
. Raisone par l'absurde, si \cap Im(u^n)) et
et 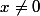 donc
donc  n'est pas invertible, alors il existe
n'est pas invertible, alors il existe 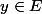 tel que
tel que =x) c'est pas difficil epreuver que
c'est pas difficil epreuver que  est une base de
est une base de  , tu arriveras à une contradiction. Bonne chance!.
, tu arriveras à une contradiction. Bonne chance!.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
