Forme indéterminée 1^{infini}
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Waax22951
- Membre Relatif
- Messages: 442
- Enregistré le: 29 Mai 2013, 16:32
- Localisation: Deux-Sèvres (79) // Paris (75)
-
par Waax22951 » 13 Déc 2014, 18:17
Bonjour,
Je me pose une petite question qui pourrait m'être utile plus tard, et donc je vous la demande pour aller plus vite: Existe-t-il des méthodes pour déterminer des limites de formes idéterminées du type
?
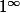
Je m'explique: on peut montrer, par exemple, qu'on a:
[CENTER]
^n=e)
[/CENTER]
Mais comment le montrer ? Il semblerait que cela soit possible avec un niveau de terminale puisque j'ai vu certains problèmes ouverts qui se rapprochaient ça..
Merci d'avance et bonne soirée !
-
Wataru
- Membre Naturel
- Messages: 24
- Enregistré le: 29 Aoû 2014, 16:11
-
par Wataru » 13 Déc 2014, 19:06
Salut,
x^y = exp(yln(x))
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
par tototo » 14 Déc 2014, 20:11
Bonjour
Demonstration:
(1+1/n)^n=exp(n(ln(1+1/n)) or en faisant un développement limité, ln(1 + 1/n) = 1/n + o(1/n) (ce qui veut dire que n(ln(1+1/n)) tend vers 1) Donc (1+1/n)^n=exp(n(ln(1+1/n)) -> exp(1) = e
-
coote
- Membre Relatif
- Messages: 138
- Enregistré le: 26 Avr 2012, 01:15
-
par coote » 14 Déc 2014, 23:12
Waax22951 a écrit:Bonjour,
Je me pose une petite question qui pourrait m'être utile plus tard, et donc je vous la demande pour aller plus vite: Existe-t-il des méthodes pour déterminer des limites de formes idéterminées du type
?
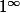
Je m'explique: on peut montrer, par exemple, qu'on a:
[CENTER]
[/CENTER]
Mais comment le montrer ? Il semblerait que cela soit possible avec un niveau de terminale puisque j'ai vu certains problèmes ouverts qui se rapprochaient ça..
Merci d'avance et bonne soirée !
salut,
si, il y a le changement de variable
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
par paquito » 15 Déc 2014, 10:56
Salut!
Tu peux établir le d.l. qui t'intéresse; il faut juste savoir intégrer par parties:
Pour
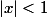
, on pose
=\bigint_{0}^{x}\frac{(x-t)^2}{2!}\frac{2}{(1+t)^3}dt)
en intégrant
)
successivement 3 fois dont 2 par parties, montrer que::
=x- \frac{x^2}{2} +I(x))
;
En remarquant que
|}{x^2}\leq|\bigint_{0}^{x}\frac{(x-t)^2}{x^2}\frac{1}{(1+t)^3}dt|\leq |\bigint_{0}^{x}\frac{1}{(1+t)^3}dt|\leq\frac{1}{2}(1-\frac{1}{(1+x)^3}).)
et en posant
=\frac{I(x)}{x^2})
, on obtient le d.l à l'ordre de
)
au voisinage de 0:
=x- \frac{x^2}{2} +x^2\epsilon(x))
, avec
=0)
Cette méthode permet d'obtenir tous les développements usuels, si f est suffisament régulière en 0, on part de :
=\bigint_{0}^{x}\frac{(x-2)^n}{n!}\n^{(n+1)}(t)dt)
et une relation apparaît vite.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
