Rang d'un systéme

[yoo]

bonjour je ne comprend pas à quoi ça sert de calculer le rang d'un systéme d'équations merci d'avance

[jose_latino]

C'est util pour savoir comme il sera l'ensemble de solutions. S'il existe solution: Le rang est égal au numéro d'incognites, si est seulement si la solution est unique.
Pour avoir une solution d'un système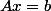 (*), où et (cela est équivalent à un système de m-équations et n-incognites), il faut trouver une solution particulaire de (*) et résoudre le système homogène associé: 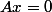(**). La dimension du sous-espace solution de (**) est . J'espère t'avoir aidé. Bon courage! :zen:

[Alexandre_de_Prepanet]

Bonjour Yoo,

Le calcul du rang d'un système d'équation te permet de déterminer le "degré de liberté" de ce système.

Autrement dit, pour un système de n équations à n inconnus, le calcul du rang te permet de dire si ce sytème admet un n-uplet solution , une infinité de n-uplets solutions, ou aucun n-uplet solution.