Limite de fonction :

[quhe]

Bonsoir,

Je dois trouver les limites en + et - l'infini des deux fonctions suivantes :


f(x)=

g(x)=


Sauf que je ne peux pas remplacer les x par des infinis.... Alors comment je peux faire ?

Cordialement,

[capitaine nuggets]

Salut !

Pour :
- En , il n'y a pas de problème.
- Pour , montre qu'en factorisant par , on a :
[CENTER][/CENTER]

Pour g :
Rappelle toi que "" donne et "" donne :+++:

[chan79]

salut



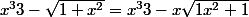
Factorise

Edit: un peu comme ci-dessus... trop lent :zen:

[quhe]

en -l'infini :

la limite de x³/3 est -inf
la limite de sqrt(x²+1) est 0


donc la limite de f est -inf c'est ça ?

[chan79]

en -l'infini :

la limite de x³/3 est -inf
la limite de sqrt(x²+1) est 0


donc la limite de f est -inf c'est ça ?

la limite de en - inf est +inf

[quhe]

donc on a une forme indéterminé car ça fait :

-inf + inf

Comment je peux faire ?

[masque gazé]

Salut

Utilise la forme conjuguée:



En effet: (a+b)(a-b)= et

[chan79]

donc on a une forme indéterminé car ça fait :

-inf + inf

Comment je peux faire ?

pour -inf, il n'y a pas de forme indéterminée

[sxmwoody]

pour -inf, il n'y a pas de forme indéterminée

bonjour de sxmwoody:
compléments qui vous sera bien utiles:
1) un polynôme , à l'inf. se comporte comme son terme de plus haut degré , d'où la méthode : mettre ce terme en facteur , de façon à faire apparaitre des termes en 1/x ;1/x^2;...qui , quand x tend vers inf , tendent vers 0.
2) 4 formes indéterminées à connaitre : +inf-inf ; inf/inf ; 0/0 ; infx0 et la façon de lever ces indéterminations (cours terminales S)

[quhe]

Pour g j'admet avoir un peu de mal en -inf.

En effet, limx=+inf limsqrt(x^2+1)=-inf donc par produit de suite de référence

limg(x)=+inf

Ce qui ne colle pas avec le graphique de g(x) ..... :mur:

Une idée ?

[chan79]

Pour g j'admet avoir un peu de mal en -inf.

Quand x tend vers , tend vers

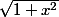
tend vers

tend vers

donc tend vers (pas de forme indéterminée)

[quhe]

je parlais de g(x) pas de f(x). Il y a une forme indéterminé en -inf avec la limite de g(x).....

Comment faire ?

Cordialement,

[HTML]Pour g j'admet avoir un peu de mal en -inf.

En effet, limx=+inf limsqrt(x^2+1)=-inf donc par produit de suite de référence

limg(x)=+inf

Ce qui ne colle pas avec le graphique de g(x) .....

Une idée ?[/HTML]

[quhe]

petit up...