Valeur propre

[jujudu597]

Bonjour,

j'aurais une question (simple je pense) mais que je n'arrive pas à comprendre xD
jspr que vous pourriez m'aider!

Si j'ai un endomorphisme qui va de dans (avec sa matrice associée).
Soit valeur propre de . Alors pourquoi ceci est équivalent à .

[jujudu597]

Pour la première implication,
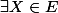
valeur propre de donc , non nul tel que .
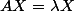
Donc
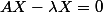
D'ou
Et après je sais pas trop comment conclure.

[Ben314]

Salut,
Ça, ça signifie très exactement que le vecteur X est dans le Noyau de A (tu as vu ce qu'était un noyau ?)
Donc ker(A) n'est pas réduit au vecteur nul (vu que X est non nul) ce qui montre que A n'est pas injective donc pas bijective donc de déterminant nul.

Pour la réciproque, tu recopie tout ça en partant du bas vers le haut (en fait on a raisonné par équivalence partout, mais c'est pas con de le vérifier)

[jujudu597]

Salut,
Ça, ça signifie très exactement que le vecteur X est dans le Noyau de A (tu as vu ce qu'était un noyau ?)
Donc ker(A) n'est pas réduit au vecteur nul (vu que X est non nul) ce qui montre que A n'est pas injective donc pas bijective donc de déterminant nul.

Pour la réciproque, tu recopie tout ça en partant du bas vers le haut (en fait on a raisonné par équivalence partout, mais c'est pas con de le vérifier)

Hmm bijective veut dire de déterminant non nul?

[Ben314]

Hmm bijective veut dire de déterminant non nul?

Ben... oui, le "déterminant", ça détermine si une matrice est inversible ou pas, c'est a dire si l'application linéaire associée est bijective ou pas.

[jujudu597]

Hmm bijective veut dire de déterminant non nul?

Ah ouiii bijective ou inversible pour la matrice!!

Merci bcp Ben314!
Une fois de plus tu m'es d'une grande aide ^^