Nombre d'application entre deux ensembles

[bandre93]

Bonsoir,
je me demandais comment démontrer, de manière assez formelle, que le nombre d'applications entre un ensemble fini F et l'ensemble des naturels N est N^F ?

Merci d'avance pour vos réponses :)

[capitaine nuggets]

Bonsoir,
je me demandais comment démontrer, de manière assez formelle, que le nombre d'applications entre un ensemble fini F et l'ensemble des naturels N est N^F ?

Merci d'avance pour vos réponses

A moins que je ne dise une bêtise, ce que tu dis, n'a aucun sens.
Le nombre d'éléments d'un ensemble, n'est pas égale à un ensemble.

Par contre, on a .

En effet, est équipotent à .
A l'aide d'un raisonnement par récurrence, tu peux montrer que quel que soit , est équipotent à .
Cela demande avant d'avoir montrer l'équipotence entre et pour montrer l'hérédité :+++:

[bandre93]

A moins que je ne dise une bêtise, ce que tu dis, n'a aucun sens.
Le nombre d'éléments d'un ensemble, n'est pas égale à un ensemble.

Tout à fait ,désolé je voulais dire par là que la cardinalité de l'ensemble des applications de F dans N est N^F ...

[capitaine nuggets]

Tout à fait ,désolé je voulais dire par là que la cardinalité de l'ensemble des applications de F dans N est N^F ...

C'est pas grave, j'ai juste voulu souligner le machin, on s'est compris :lol3:

[bandre93]

merci pour ta réponse en tout cas !

[beagle]

merci pour ta réponse en tout cas !

et donc cardinal de N,
bref au total,cela ne dépend pas de F
et N dans N sera idem, non?

[capitaine nuggets]

Salut !

et donc cardinal de N,
bref au total,cela ne dépend pas de F
et N dans N sera idem, non?

C'est une question que tu te pose où tu la poses bandre93 ? :hein:

[beagle]

Salut !

C'est une question que tu te pose où tu la poses bandre93 ? :hein:

surtout à bandre93,
que voulait-il faire avec cela?
= que fait-on d'une formule avec F qui ne dépend finalement pas de F,

PS:j'enlève le reste qui est stupide, car je redis en moins bien ce que tu avais déjà écrit,
et que j'ai lu trop vite.

[Ben314]

Salut,
C'est... on ne peut plus "couillon" :
Tu as un ensemble fini de cardinal .
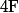A toute fonction , on peut (super subtilement) associer l'élément et c'est pas la peine d'être grand druide pour voir que est une bijection de l'ensemble des fonctions de dans 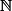dans l'ensemble .

Et c'est ce "très couillon là" qui justifie, qu'en général, l'ensemble des applications de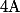 dans 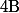est noté .

[bandre93]

que fait-on d'une formule avec F qui ne dépend finalement pas de F,

Pourquoi la formule ne dépend elle pas de F ?

[bandre93]

est une bijection de l'ensemble des fonctions de dans dans l'ensemble .

ça ne me parait pas aussi trivial de dire que est une bijection, peux-tu m'éclairer ?

[capitaine nuggets]

Pourquoi la formule ne dépend elle pas de F ?

D'après ce qui a été dit :

Quel que soit , et ont même cardinal :+++:

Du coup, quel que soit le cardinal de l'ensemble fini , le cardinal de vaut toujours celui de (d'où l'indépendance).

Pour la culture, on note :+++:)

[Ben314]

ça ne me parait pas aussi trivial de dire que est une bijection, peux-tu m'éclairer ?

Réfléchis 15 secondes :
Si on se donne un n-uplet existe t-il une application

Si oui, est-elle unique ?