Bonjour j'ai 2-3 nature de séries à trouver mais je bloque, pouvez vous m'aidez ?
1. Un = (1 + n + n^2 ) / n!
2. Un = ln ( (1 + tan (1/n) ) / (1 - tan(1/n) )
3. Un = sin ( (pi*n^2) / (n + 1 ))
Pour la 1), la règle d'Alembert est appropriée ?
Séries numériques
11 messages
- Page 1 sur 1
Salut,
Pour la 3em,) ce n'est pas du tout évident à première vue d'estimer
ce n'est pas du tout évident à première vue d'estimer  .
.
A mon avis, vu que, pour tout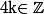 ,
, =(-1)^k\sin(\varepsilon)) , cela doit inciter à écrire
, cela doit inciter à écrire  sous la forme
sous la forme  avec
avec 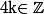 .
.
Comme on a donc
on a donc 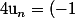^{n-1}\sin\Big(\frac{\pi}{n+1}\Big)\ (*)) ce qui prouve que
ce qui prouve que  et même que
et même que  qui est le terme général d'une série divergente donc la série
qui est le terme général d'une série divergente donc la série  n'est pas absolument convergente.
n'est pas absolument convergente.
Mais, elle peut quand même être convergente, et vu la tête de la formule (*), il semble adapté d'utiliser le critère concernant les séries alternées...
Pour la 3em,
A mon avis, vu que, pour tout
Comme
Mais, elle peut quand même être convergente, et vu la tête de la formule (*), il semble adapté d'utiliser le critère concernant les séries alternées...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Et je rajouterais que, concernant le "reste", ben ça servait à rien de développer (n+1)²+(n+1)+1, ni même de l'écrire d'ailleurs.
Vu que P(n)=n²+n+1 est un polynôme, P(n+1)/P(n) tend vers 1 lorsque n tend vers l'infini car P(n+1) et P(n) ont trivialement le même terme de plus haut degré.
Vu que P(n)=n²+n+1 est un polynôme, P(n+1)/P(n) tend vers 1 lorsque n tend vers l'infini car P(n+1) et P(n) ont trivialement le même terme de plus haut degré.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
