Fonction dérivée: besoin de quelques eclaircissement

[paquito]

Bonjour,

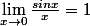
Tout repose sur une démonstration géométrique de ; c'était ce qu'on faisait en première S quand on démontrait encore quelque chose, mais maintenant tout est admis! Même si la démonstration n'a pas la même rigueur que celle qui découle de , c'était quand même une argumentation qui tenait la route.

ce que je veux dire, c'est que les élève de première S vont très vite abandonner pour calculer ; mais par contre en T°, ils devront reconnaître ou comme des nombres dérivés alors que pour les deux fonctions en question, la dérivée aura été admise (la dérivée de la bijection réciproque n'est plus au programme de même la formule (fou)'=u'f'(u)).

Donc on est parfaitement d'accord, cette définition de f'(x) est fondamentale et doit être connue, mais il est hors de question de l'utiliser pour calculer des dérivées, hormis celles qui servent de résultats de base.

[Ben314]

Juste une remarque (sans grande importance en fait) :

Il y a une différence de "niveau" (donc de quantité de truc a admettre) entre les deux limites



La première n'utilise pas la "vitesse de parcours sur le cercle trigo." des fonction sin et cos : si on changait la "vitesse de parcours", c'est à dire si on remplaçait et par et où elle resterai vrai.
Donc on peut par exemple la démontrer en admettant uniquement le fait que le chemin le plus court entre deux points est la ligne droite ce qui signifie que, si I=(1,0) et M=(cos(h),sin(h)), alors la corde IM est plus courte que l'arc h.

Par contre, assez clairement, la deuxième limite est liée à la "vitesse de parcours" particulière des fonctions sin et cos donc elle ne peut pas se déduire de la première (alors que la première se déduit facilement de la seconde) et elle demande un encadrement "plus fin" du lien entre l'arc IM et la corde h : d'une façon ou du autre il faut maintenant "admettre" que non seulement la corde est plus petite que l'arc, mais qu'elle lui est équivalente pour h petit.

Je le redit : c'est sans grand intérêt...

[paquito]

De toutes façons, on donne en TS les dérivées de sin et cos sans instructions particulières et comme la seule formule de trigo donnée en 1°S dans le chapitre produit scalaire est cos(ab)=cos(a)cos(b)+sin(a)sin(b) et que de plus parité et périodicité ne sont plus d'actualité, on n'est pas près d'avoir l'étude d'une fonction trigo au bac; donc inutile de se faire du soucis.

[sxmwoody]

bonjour ...plus au bac ? bien dommage...Ne pas se faire du souci ? Oh que si !, nos futurs ingénieurs vont avoir un bagage bien léger...pas rassurant de leur confier notre avenir...

[zygomatique]

sans parler d'équivalent on peut très bien encadrer la longueur de l'arc AB par AB et AC = tan(x)

et conclure tout de même puisque tan(x) --> 0

[paquito]

Tout ça a déjà été dit,il n'y a pas de problème au niveau de l'enseignement,mais sinon,comment est défini la longueur d'un arc, une aire.....ce qui était suffisant et convaincant avec nos vieux élèves mais qui est totalement hors programme actuellement et qui de toute façon reste du bricolage( pas con d'accord.) n'est même plus d'actualité...

[paquito]

bonjour ...plus au bac ? bien dommage...Ne pas se faire du souci ? Oh que si !, nos futurs ingénieurs vont avoir un bagage bien léger...pas rassurant de leur confier notre avenir...

Tu mets l'accent où il va y avoir un très gros problème! Mais les chinois, les indiens, etc.... forment des ingénieurs à la pelle.....

[Luc]

Juste une remarque (sans grande importance en fait) :

Il y a une différence de "niveau" (donc de quantité de truc a admettre) entre les deux limites

En gros la première formule est d'ordre 1, l'autre d'ordre 0.

[Ben314]

sans parler d'équivalent on peut très bien encadrer la longueur de l'arc AB par AB et AC = tan(x)

Tu n'est effectivement pas obligé d'utiliser le terme "d'équivalents", mais ton encadrement prouve en fait que l'arc est équivalent à la corde.
Ce que je voulais juste dire, c'est qu'en plus de la minoration IM<=h assez façile à "admettre", il faut aussi trouver un majorant qui peut être un peu n'importe quoi pourvu qu'il donne l'équivalence entre la corde et l'arc pour h petit (une fois que toi, le prof., a vu que ça donnait bien cette équivalence, il n'est nul besoin d'utiliser le mot en question avec les élèves)
Donc, pour revenir a ta majoration de h par tan(h), elle est (a mon avis) un peu plus difficile a "admettre" que la minoration par IM qui résulte du fait admis depuis le collège que "le plus court chemin est la ligne droite".

Tu le présenterais comment a des élèves le fait que h<=tan(h) pour que ça semble assez "normal" ?

(bis) c'est pas bien important...

[zygomatique]

Tu n'est effectivement pas obligé d'utiliser le terme "d'équivalents", mais ton encadrement prouve en fait que l'arc est équivalent à la corde.
Ce que je voulais juste dire, c'est qu'en plus de la minoration IM<=h assez façile à "admettre", il faut aussi trouver un majorant qui peut être un peu n'importe quoi pourvu qu'il donne l'équivalence entre la corde et l'arc pour h petit (une fois que toi, le prof., a vu que ça donnait bien cette équivalence, il n'est nul besoin d'utiliser le mot en question avec les élèves)
Donc, pour revenir a ta majoration de h par tan(h), elle est (a mon avis) un peu plus difficile a "admettre" que la minoration par IM qui résulte du fait admis depuis le collège que "le plus court chemin est la ligne droite".

Tu le présenterais comment a des élèves le fait que h<=tan(h) pour que ça semble assez "normal" ?

(bis) c'est pas bien important...

oui effectivement ... alors prendre le segment tangent au milieu de l'arc AB ....

enfin bof ...

[Ben314]

Ton h, il se mesure sur un truc "courbe" et pas en ligne droite, donc quel que soit le majorant, il va falloir a un moment dire qu'un truc courbe est plus court qu'autre chose et ça sera forcément pas bien formel.

Perso, je me demande si je ne majorerais h pas par sin(h)+(1-cos(h)) qui est le trajet parcouru en allant de I a M en suivant les parallèles aux axes (intuitivement plus long).

[sxmwoody]

Tu mets l'accent où il va y avoir un très gros problème! Mais les chinois, les indiens, etc.... forment des ingénieurs à la pelle.....

=sxmwoody

tout à fait d'accord! "Les puissants de l'ombre" qui dirigent au niveau de la planète savent à qui s'adresser pour leurs problèmes techniques : pour l'informatique : les pakistanais ; pour les maths : les indiens , 2 fois plus performants et 4 fois moins chers ...
Pour les langues ,bien sûr l'anglais en espérant ne pas avoir à programmer en chinois dans un avenir qui arrive à grand pas ! (NB : les pictogrammes , cela s'apprend assez vite mais les orientaux font leurs "business" entre eux !!!)