Mago a écrit:Bonjour/bonsoir,
Je m'adresse a vous car j'ai eu un doute pendant que je faissait mes exos sur les fonctions dérivées, ou plutot le nombre dérivé.
en effet nous ne somme pas encore "arrivés" sur la "découverte" de la fonction dérivée, mais nous devons montrer que f est dérivable en un point donné pour une fonction donné. Le probleme réside ici: je sais que pour la fonction carré on procède de la manière suivante:
lim avec h->0 : [ f(x+h)-f(x) ]/h
je voudrais savoir alors si cela s'applique pour toutes les fonctions ou non je vous remercie d'avance de votre aide

Oui cela s'applique à toutes les fonctions!
Newton et Leibniz ont créé ce calcul des dérivées dans les années 1670. L'idée est que

est un petit accroissement de la variable

, et on souhaite mesurer de combien varie

lorsque la variable

passe de la valeur

à
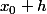
. La réponse est :

varie
proportionnellement à

, le coefficient de proportionnalité étant exactement (en fait, approximativement, car on a négligé les infiniment petits d'ordre supérieur) le nombre dérivé de

en

. Newton appelle ces petits accroissements des "fluxions", Leibniz des "infiniment petits".
Par exemple, si

mesure le temps et
)
mesure la position d'une voiture au temps

, le nombre dérivé de

en

s'interprète comme la vitesse instantanée de la voiture passant au temps

par le point repéré par le nombre
)
.
Voici comment Newton calculerait la fonction dérivée de la fonction

.
1. On remplace

par

et

par
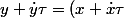^2)
.

et

désignent les "fluxions" de

et

, ce sont des vitesses de variation, et

est une petite durée pendant laquelle les quantités

et

varient.
2. On développe le carré par le binôme de Newton (encore lui!) :
^2=x^2+2x\dot x \tau+(\dot x \tau)^2)
.
3. On retranche la valeur initiale de la fonction :
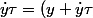 - y = x^2+2x\dot x \tau+(\dot x \tau)^2 -x^2 = 2x\dot x \tau+(\dot x \tau)^2)
4. On divise par

:
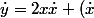^2 \tau)
5. On néglige le terme
^2 \tau)
car

est très petit.
6. Il reste

donc

7. On a donc montré que la dérivée de
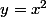
est

! (ouf)
Voici comment Leibniz calculerait la même dérivée :
1.
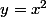
2. On calcule la petite variation de y en fonction de la petite variation de x
^2-x^2 = 2x dx + (dx)^2)
3. On simplifie

4. On néglige
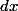
par rapport à

:

5. On a bien le même résultat, la dérivée de
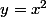
est

!
La méthode de Leibniz est très utilisée notamment en physique, cela s'appelle le calcul différentiel.
Luc
