Binôme de Newton et matrice
29 messages
- Page 1 sur 2 - 1, 2
Binôme de Newton et matrice
Bonjour,
Je suis complètement bloquée sur un exercice, je viens donc à la recherche d'un coup de main !
J'ai deux matrices,
B =
3 2 2 2
2 3 2 2
2 2 3 2
2 2 2 3
et C =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
On a B = 2C + I
et il faut calculer B^n en utilisant le binôme de Newton.
J'ai remarqué que C^n = 4^(n-1) * C mais je sais pas si ça aide...
Je sais que (2C + I)^n = Somme (k=0,n) de (k parmi n) * (2C)^k mais je n'arrive pas à aller plus loin. Je n'arrive pas à simplifier l'expression si je développe la formule...
Help ? ^^
(et désolée pour l'écriture de l'équation, je ne sais pas comment avoir la bonne syntaxe sur le forum)
Merci !
Je suis complètement bloquée sur un exercice, je viens donc à la recherche d'un coup de main !
J'ai deux matrices,
B =
3 2 2 2
2 3 2 2
2 2 3 2
2 2 2 3
et C =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
On a B = 2C + I
et il faut calculer B^n en utilisant le binôme de Newton.
J'ai remarqué que C^n = 4^(n-1) * C mais je sais pas si ça aide...
Je sais que (2C + I)^n = Somme (k=0,n) de (k parmi n) * (2C)^k mais je n'arrive pas à aller plus loin. Je n'arrive pas à simplifier l'expression si je développe la formule...
Help ? ^^
(et désolée pour l'écriture de l'équation, je ne sais pas comment avoir la bonne syntaxe sur le forum)
Merci !
Salut,
Attention tout de même a bien justifier qu'on a le droit d'appliquer la formule du binôme de Newton dans ce contexte là : la formule (A+B)^n=... ne s'applique que si AB=BA (ce qui est bien le cas ici, mais qui n'est pas vrai en général pour deux matrices quelconques)
Dans ta somme, k prend (au début) la valeur 0 et, pour n=0, ta formule C^n = 4^(n-1) * C est fausse.
Attention tout de même a bien justifier qu'on a le droit d'appliquer la formule du binôme de Newton dans ce contexte là : la formule (A+B)^n=... ne s'applique que si AB=BA (ce qui est bien le cas ici, mais qui n'est pas vrai en général pour deux matrices quelconques)
Attention, là il y a une petite erreur (mais qui fait quand même que ton résultat va être faux)flatozore a écrit:B^n= C * sum ((k parmi n) * 2^k * 4^(k-1))
Dans ta somme, k prend (au début) la valeur 0 et, pour n=0, ta formule C^n = 4^(n-1) * C est fausse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'ai rajouté un truc (plus grave) dans le post. précédent.
Sinon, concernant ta somme, ne pas oublier que le binôme de Newton s'applique à... plein de truc (réels, complexes,...)
Et que la formule "de base" te dit que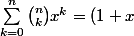^n) pour tout réel/complexe x.
pour tout réel/complexe x.
et dans cette formule, si tu prend x=8...
Sinon, concernant ta somme, ne pas oublier que le binôme de Newton s'applique à... plein de truc (réels, complexes,...)
Et que la formule "de base" te dit que
et dans cette formule, si tu prend x=8...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ah oui ok, je comprends maintenant ce que voulait dire Mr23 ! merci
Dans ma formule de départ, j'ai sum de k=0 à n, (k parmi n) * (2C)^k.
Donc, pour le cas k=0, ça fait 0, donc ma somme devient :
sum de k=1 à n, (k parmi n) * (2C)^k, non ?
Sauf que là, je ne peux plus utiliser la formule de base du binôme merde ><
Mon énoncé précise que n E N*
Dans ma formule de départ, j'ai sum de k=0 à n, (k parmi n) * (2C)^k.
Donc, pour le cas k=0, ça fait 0, donc ma somme devient :
sum de k=1 à n, (k parmi n) * (2C)^k, non ?
Sauf que là, je ne peux plus utiliser la formule de base du binôme merde ><
Mon énoncé précise que n E N*
non non...flatozore a écrit:Dans ma formule de départ, j'ai sum de k=0 à n, (k parmi n) * (2C)^k.
Donc, pour le cas k=0, ça fait 0,
Quand on utilise la formule du binôme de Newton, quelque soit le contexte, ?^0 désigne systématiquement l'élément neutre (pour le produit) de l'ensemble dans lequel on travaille. Donc ici, le C^0 désigne la matrice identité I.
(attention au fait que, dans d'autres contexte, on on n'a pas forcément la même convention sur ce que désigne C^0)
Concernant ton "résultat final", vérifie le en prenant (au moins) n=1 voire même n=2 pour plus de sureté (n=0 risque d'être un cas "vicieux" mais tu peut quand regarder ce que donne ton résultat dans ce cas là, par curiosité...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Décidément, je suis à la ramasse aujourd'hui moi ! Je me suis arrêtée au fait que (0 parmi n), ça faisait 0...
Bon, je vais essayer de pas dire de connerie cette fois...
Dans le cas k=0 :
ça nous donne donc 0 * I -> matrice nulle
Donc j'avais fait une (grosse) erreur, mais le résultat final reste bon ?
Merci bcp de votre aide à tous les 2 en tout cas
Bon, je vais essayer de pas dire de connerie cette fois...
Dans le cas k=0 :
ça nous donne donc 0 * I -> matrice nulle
Donc j'avais fait une (grosse) erreur, mais le résultat final reste bon ?
Merci bcp de votre aide à tous les 2 en tout cas
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
