Besoin d'aide svp (fonctions première s)
16 messages
- Page 1 sur 1
besoin d'aide svp (fonctions première s)
bonjour, :we:
on considère les fonctions f eg définies sur R par
f(x) = barre verticale -2x-5 barre verticale et g(x) = bv x +2 bv - bv 3x-4 bv
exprimer f(x) et g(x) sans utiliser les barres de valeur absolue suivant les valeurs de x dans R
dresser le tableau de variation de f et de g
Qui peut résoudre cet enonce avnt le vendredi 5/12/2014
merci d'avance
on considère les fonctions f eg définies sur R par
f(x) = barre verticale -2x-5 barre verticale et g(x) = bv x +2 bv - bv 3x-4 bv
exprimer f(x) et g(x) sans utiliser les barres de valeur absolue suivant les valeurs de x dans R
dresser le tableau de variation de f et de g
Qui peut résoudre cet enonce avnt le vendredi 5/12/2014
merci d'avance
Salut !
Reviens à la définition de la valeur absolue d'un réel :
:
[CENTER]
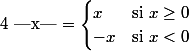 [/CENTER]
[/CENTER]
Commence par résoudre les équations=0) et
et =0) , puis suivant les valeurs de
, puis suivant les valeurs de  , tu pourras conclure :+++:
, tu pourras conclure :+++:
lol21 a écrit:bonjour, :we:
On considère les fonctionset
définies sur
par
et
exprimeret
sans utiliser les barres de valeur absolue suivant les valeurs de
dans
. Dresser le tableau de variation de
et de
Qui peut résoudre cet enonce?
merci d'avance
Reviens à la définition de la valeur absolue d'un réel
[CENTER]
Commence par résoudre les équations
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
lol21 a écrit:-2x - 5 si -2x-5 > 0
-(2x-5) si -2x-55
-2x+5 si x 2/5
pour le premier c'est ca ?
L'idée est bonne mais il y a des erreurs dans les conditions "si" :++:
Quelle est la solution de l'équation f(x)=0 ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
lol21 a écrit:Quelles sont ces erreurs ? :/
La solution de f(x) c'est 2/5 non ?
Ben ... non :ptdr:
Calcule f(2/5) pour t'en convaincre :+++:
lol21 a écrit:eooooh
:hum: Inutile, on te répondra quand on te répondra.
Tout ce que tu vas arriver à faire, c'est faire fuir ceux qui voudrais bien t'aider :marteau:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
lol21 a écrit:loldsl.

alors je me suis tromper où ?
Au lien d'attendre naïvement un réponse que tu pourrais trouver presque instantanément, pose-toi et réfléchis deux seconde :++:
Je t'ai donné la définition de la valeur absolue d'un réel. Quand s'annule-t-elle ?
Fais-en de même avec f :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Au lien d'attendre naïvement un réponse que tu pourrais trouver presque instantanément, pose-toi et réfléchis deux seconde :++:
Je t'ai donné la définition de la valeur absolue d'un réel. Quand s'annule-t-elle ?
Fais-en de même avec f :+++:
aaaah mais je me suis trompé c'est 5/2 pas 2/5
f(x)=0
f(x)= -2x+5
f(x) = -2*5/2 + 5
f(x) = 0
lol21 a écrit:aaaah mais je me suis trompé c'est 5/2 pas 2/5
f(x)=0
f(x)= -2x+5
f(x) = -2*5/2 + 5
f(x) = 0voilà .
:doh: tu t'emmêle : f(x)=-2x+5 ou -2x-5 ? :doh:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
lol21 a écrit:et pour la deuxième je vais essayer
x+2 - 3x-4
x+2 si x+2 >0
-(x-2) si x +2 0
-x+2 si x+2 -2
-x+2 si x0
-3x+4 si 3x-4 4
-3x-4 si 3x 4/3
-3x-4 si x < 4/3
et après c'est
-2 - 4/3 = -10/3
c'est ca ?
Bonjour,
Non, il faut distinguer différents cas mais pour que ce soit plus simple, l'idéal est de rpésenter tout ceci sous forme d'un tableau.
Ce n'est pas obligatoire mais plus simple.
Recommence et inspire toi de l'exemple ci-dessous, cela devrait suffire pour résoudre tes problèmes.
Exemple de simplifications avec des valeurs absolues
J-F L
maths-lycee fr a écrit:Bonjour,
Non, il faut distinguer différents cas mais pour que ce soit plus simple, l'idéal est de rpésenter tout ceci sous forme d'un tableau.
Ce n'est pas obligatoire mais plus simple.
Recommence et inspire toi de l'exemple ci-dessous, cela devrait suffire pour résoudre tes problèmes.
Exemple de simplifications avec des valeurs absolues
J-F L
^je n'arrive pas à faire le tableau je ne comprends pas
lol21 a écrit:^je n'arrive pas à faire le tableau je ne comprends pas
Bonjour,
Il s'agit d'étudier le signe de chacune des expressions x+2 et 3x-4 comme si on faisait un tableau pour étudier le signe d'un produit.
Ce qui signifie par exemple pour le terme |x+2| que l'on a:
[HTML]
x -oo -2 +oo
x+2 - 0 +
|x+2| -x-2 0 x+2
[/HTML]
car si x+2<0 on a |x+2|=-(x+2)=-x-2
Il faut refaire la même chose avec 3x-4 en combinant les deux tableaux comme dans l'exemple
Ensuite, il faut calculer |x+2|-|3x-4| dans ls différents cas.
Ici, il y aura x<-2 -2<x<4/3 et 4/3<x
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
