Prolongement par continuite

[amad9720]

Bonjours a tous,
Je prépare mon Dst de maths pour lundi et j'aimerai si possibles avoir de l'aide sur les exercices sur lesquelles je bloque dans mes révisions .

1/Peut-on prolonger par continuit ;)e en 0 les fonctions d ;)efinies sur [;)1,0[;)]0,1] par
xln|x|, xln|sinx|?

2/Peut-on prolonger par continuit ;)e la fonction la fonction f(x) = e^;)( 1/sinx )^2 ?

merci pour votre temps!

[MC91]

Bonjour,

Pour xln|x|, je dirai oui, puisque la limite de cette fonction en 0 vaut 0 (par croissance comparée).
Attends quand même la confirmation d'une autre personne, car je ne suis pas une pro !!

[Ncdk]

En fait,

f peut être prolongé par continuité en lorsque f admet une limite finie quand

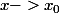
Donc on peut dire : et donc pour prolonger f par continuité en , on pose

[zaidoun]

Toutes les fonctions sont prolongeables par continuité.

[chan79]

salut
oui, on envisage deux cas: x>0 et x<0 . Dans les deux cas, la limite est 0

[amad9720]

je vous remercie pour vos indication .