Variance loi hypergéométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 27 Nov 2014, 23:49
par joanie58 » 27 Nov 2014, 23:49
Bonjour,
je dois montrer que la variance d'une loi hypergéométrique X ~ H(N, p, n) est donner par
 = np(1-p) \frac{N-n}{N-1})
mais je ne sais pas trop comment m'y prendre
Je sais que
 = E (X^2) - (E(X))^2)
et j'ai réussi a montrer que E(X) = np
mais pour
)
je ne suis pas capable d'utiliser le même principe que j'ai utiliser pour E(X)
Pouvez-vous m'aider ?
Merci
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 28 Nov 2014, 00:12
par SLA » 28 Nov 2014, 00:12
joanie58 a écrit:Bonjour,
je dois montrer que la variance d'une loi hypergéométrique X ~ H(N, p, n) est donner par
 = np(1-p) \frac{N-n}{N-1})
mais je ne sais pas trop comment m'y prendre
Je sais que
 = E (X^2) - (E(X))^2)
et j'ai réussi a montrer que E(X) = np
mais pour
)
je ne suis pas capable d'utiliser le même principe que j'ai utiliser pour E(X)
Pouvez-vous m'aider ?
Merci
Ha? comment as-tu calculé EX alors? N'as-tu pas une formule du type
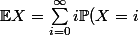)
?
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 28 Nov 2014, 03:00
par joanie58 » 28 Nov 2014, 03:00
SLA a écrit:Ha? comment as-tu calculé EX alors? N'as-tu pas une formule du type
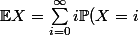)
?
non justement je me suis fortement inspirer de cet démo:
http://fr.wikipedia.org/wiki/Loi_hyperg%C3%A9om%C3%A9trique J'ai essayer de montrer
)
avec la somme d'indicatrice ..mais ce ne fut pas très concluant

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Nov 2014, 12:24
par Ben314 » 28 Nov 2014, 12:24
Salut,
joanie58 a écrit:J'ai essayer de montrer
)
avec la somme d'indicatrice ..mais ce ne fut pas très concluant
Pourtant, à mon avis, c'est la méthode la plus rapide pour trouver le résultat.
En reprenant les notations de wiki, on a

donc
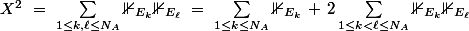
d'où
\ =\ N_A{\mathbb P}(E_1)+N_A(N_A-1){\mathbb P}(E_1\cap E_2)\ =\ \cdots)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 28 Nov 2014, 13:27
par joanie58 » 28 Nov 2014, 13:27
Ben314 a écrit:Salut,Pourtant, à mon avis, c'est la méthode la plus rapide pour trouver le résultat.
En reprenant les notations de wiki, on a

donc
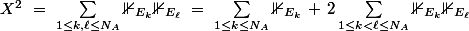
d'où
\ =\ N_A{\mathbb P}(E_1)+N_A(N_A-1){\mathbb P}(E_1\cap E_2)\ =\ \cdots)
j'ai un peu de misère à
\)
est-ce que je peux y parvenir de cette facon:
\ = {\mathbb P}(E2){\mathbb P}(E_1 | E_2) = \frac{n}{N}{\mathbb P}(E_1 | E_2))
et on a que
 = 1-{\mathbb P}(E_1^c|E_2) = 1 - \frac{ \binom{N-2}{n-1}}{\binom{N-1}{n-1}} = \frac{n-1}{N-1})
Ensuite j'aurais
\ =\frac{n}{N} \frac{n-1}{N-1}N_A(N_A-1) + np)
où

est l'événement que

ne se réalise pas
mais comme je n'arrive pas a arriver à la bonne réponse..j'imagine que ce que j'ai fait n'est pas correcte.....

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Nov 2014, 18:39
par Ben314 » 28 Nov 2014, 18:39
)
c'est la proba d'avoir tiré deux boules fixées d'avance parmi les

boules prise dans l'urne qui en contient
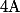
(notations de wiki) donc effectivement
=\frac{{A-2\choose n-2}}{{A\choose n}}=\frac{n(n-1)}{A(A-1)})
Et je vois pas bien l'intérêt d'utiliser des proba. conditionnelles, ni l'évènement contraire ici : un petit coup de "cas favorables/cas total" est suffisant.
On en déduit (avec
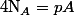
) que
\,<br />=\,pA\times\frac{n}{A}+pA(pA-1)\times\frac{n(n-1)}{A(A-1)}\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})\Big))
puis
\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})-n^2p^2\,<br />=\,npq\frac{A-n}{A-1})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Nov 2014, 18:46
par Ben314 » 28 Nov 2014, 18:46
)
c'est la proba d'avoir tiré deux boules fixées d'avance parmi les

boules prise dans l'urne qui en contient
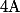
(notations de wiki) donc effectivement
=\frac{{A-2\choose n-2}}{{A\choose n}}=\frac{n(n-1)}{A(A-1)})
Et je vois pas bien l'intérêt d'utiliser des proba. conditionnelles, ni l'évènement contraire ici : un petit coup de "cas favorables/cas total" est suffisant.
On en déduit (avec
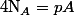
) que
\,<br />=\,pA\times\frac{n}{A}+pA(pA-1)\times\frac{n(n-1)}{A(A-1)}\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})\Big))
puis
\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})-n^2p^2\,<br />=\,npq\frac{A-n}{A-1})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 28 Nov 2014, 19:33
par joanie58 » 28 Nov 2014, 19:33
Ben314 a écrit:)
c'est la proba d'avoir tiré deux boules fixées d'avance parmi les

boules prise dans l'urne qui en contient
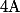
(notations de wiki) donc effectivement
=\frac{{A-2\choose n-2}}{{A\choose n}}=\frac{n(n-1)}{A(A-1)})
Et je vois pas bien l'intérêt d'utiliser des proba. conditionnelles, ni l'évènement contraire ici : un petit coup de "cas favorables/cas total" est suffisant.
On en déduit (avec
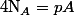
) que
\,<br />=\,pA\times\frac{n}{A}+pA(pA-1)\times\frac{n(n-1)}{A(A-1)}\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})\Big))
puis
\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})-n^2p^2\,<br />=\,npq\frac{A-n}{A-1})
ok dans le fond j'arrive a la même chose que toi jusqu'à
\,<br />=\,np+n(n-1)p(p-\frac{q}{A-1})-n^2p^2\,)
mais je ne comprend pas comment tu arrive à la dernière égalité soit np(1-p)(N-n)/(N-1)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Nov 2014, 19:46
par Ben314 » 28 Nov 2014, 19:46
Ben, tu met

en facteur et tu développe ce qu'il y a dans la parenthèse... (et tu utilise ensuite une deuxième fois le fait que
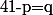
pour mettre
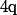
en facteur)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
je ne suis pas capable d'utiliser le même principe que j'ai utiliser pour E(X)
?
?
avec la somme d'indicatrice ..mais ce ne fut pas très concluant

c'est la proba d'avoir tiré deux boules fixées d'avance parmi les
boules prise dans l'urne qui en contient
(notations de wiki) donc effectivement
=\frac{{A-2\choose n-2}}{{A\choose n}}=\frac{n(n-1)}{A(A-1)})
) que