Transformé de fourrier d'un produit de fonctions

[razine]

Bonjour,

Il est dit sur wikipedia que le produit de deux fonctions équivaux à la convolution dans l'espace de fourrier.

J'ai un petit soucis avec le code :

f1 = [1 2];
f2 = [5 3];

ff1 = fft( f1 );
ff2 = fft( f2 );

ifft( (1/2*pi) * conv( ff1, ff2 ))

ça me retourne pas le produit, des suggestions?

[Ben314]

Salut,
Ca veut dire quoi f1 = [1 2] par exemple ?

[sinusx]

Salut,

La transformée de Fourier (TF) d'un produit de convolution est égale au produit des TF ; et vice-versa. En gros la TF transforme le produit (resp. convolution) en convolution (resp. produit).
En numérique, c'est aussi vrai, mais il y a quelques précisions.

Par défaut, la FFT représente la convolution "circulaire", puisque les algorithmes de calcul de la TF numérique supposent que le signal est périodique.
Si tu veux représenter la convolution "linéaire" par la FFT, il faut faire un "zero-padding" des signaux engagés. Ca peut se faire en calculant la FFT sur un plus grand nombre de points. Pour que la convolution circulaire soit équivalente à la convolution linéaire, le nombre de points doit être supérieur ou égal à avec 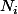la longueur des signaux.

Je suppose que la syntaxe utilisée est Matlab/Scilab, donc ça donnerait (avec ".*" le produit élément par élément) :

[FONT=Courier New]
N = length(f1)+length(f2)-1;
ifft(fft(f1,N) .* fft(f2,N))
conv(f1,f2)
[/FONT]