Complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Le Chat
- Membre Relatif
- Messages: 128
- Enregistré le: 19 Nov 2012, 23:11
-
 par Le Chat » 13 Nov 2014, 04:26
par Le Chat » 13 Nov 2014, 04:26
salut,
J'ai un exo qui me demande de résoudre l'équation suivante pour

dans C
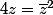
je cherche une solution simple (qui utilise une propriété des conjugués par exemple) plutôt que de remplacer z par a+bi. des idées?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Nov 2014, 08:28
par Ben314 » 13 Nov 2014, 08:28
En prenant les modules des deux cotés puis en multipliant par z pour en déduire que z(barra)^3 est un réel positif ce qui ne donne que 3 possibilités pour le module de z(barre).
(ou en prenant directement les argument des deux cotés...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 13 Nov 2014, 12:22
par zygomatique » 13 Nov 2014, 12:22
salut
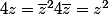
on fait la différence et on factorise ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Nov 2014, 12:58
par Ben314 » 13 Nov 2014, 12:58
Ca me semble plus "naturel" en polaire (les produit/divisions/puissances sont plus simple en polaire).
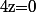
est solution et, si
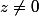
on écrit
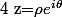
avec
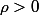
et on a :

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 13 Nov 2014, 13:42
par zygomatique » 13 Nov 2014, 13:42
Ben314 a écrit:Ca me semble plus "naturel" en polaire (les produit/divisions/puissances sont plus simple en polaire).
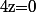
est solution et, si
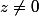
on écrit
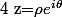
avec
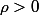
et on a :

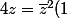 \\ 4 \bar z = z^2)
par soustraction
 = (\bar z - z)(\bar z + z) (z - \bar z)(z + \bar z + 4) = 0)
z = z* ou z + z* = -4
z est réel ou Re(z) = 2
si z est réel alors (1) z(z - 4) = 0 z = 0 ou z = 4
si z = -2 + ai alors ...
je ne pense pas que l'argument "la forme exponentielle soit plus naturelle" soit valable (en lycée) mais la justification de cet argument et la résolution très rapide sont deux arguments beaucoup plus valables (à mon sens)
car ma méthode nécessite de plus de faire une synthèse ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Le Chat
- Membre Relatif
- Messages: 128
- Enregistré le: 19 Nov 2012, 23:11
-
 par Le Chat » 14 Nov 2014, 01:03
par Le Chat » 14 Nov 2014, 01:03
zygomatique a écrit: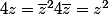
comment ça??

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Nov 2014, 01:15
par Ben314 » 14 Nov 2014, 01:15
zygomatique a écrit:je ne pense pas que l'argument "la forme exponentielle soit plus naturelle" soit valable (en lycée) mais la justification de cet argument et la résolution très rapide sont deux arguments beaucoup plus valables (à mon sens)
Je ne sais pas ce qu'il font au lycée, mais... tu as mal interprété ce que je disait.
Ce que j'ai voulu dire, c'est que lorsque tu as uniquement des produit/divisions/puissances/conjugués (et ni addition ni soustraction), il est plus naturel d'employer la forme trigo. que la forme cartésienne pour résoudre le problème.
Et, bien que ne sachant ce qu'il font au lycée, je pense que si on leur définit le module et les arguments d'un nombre complexe, on doit quand même leur montrer que les produits (et surtout les divisions et les puissances) sont bien plus simple avec ce format là qu'avec le format x+iy.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Nov 2014, 20:28
par zygomatique » 14 Nov 2014, 20:28
Ben314 a écrit:Je ne sais pas ce qu'il font au lycée, mais... tu as mal interprété ce que je disait.
Ce que j'ai voulu dire, c'est que lorsque tu as uniquement des produit/divisions/puissances/conjugués (et ni addition ni soustraction), il est plus naturel d'employer la forme trigo. que la forme cartésienne pour résoudre le problème.
Et, bien que ne sachant ce qu'il font au lycée, je pense que si on leur définit le module et les arguments d'un nombre complexe, on doit quand même leur montrer que les produits (et surtout les divisions et les puissances) sont bien plus simple avec ce format là qu'avec le format x+iy.
tout à fait d'accord ....et c'est ce que je fais .... avec les élèves qui savent calculer ....
et oui bien sur et bien d'accord avec ta première remarque ....
mais souvent avec des équations d'inconnues complexes et des coefficients réels (ou pas faut voir) les propriétés algébriques de base sont souvent suffisantes et les manipuler permettent de les apprendre ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
est solution et, si
on écrit
avec
et on a :