J'ai croisé cette propriété, qui dit que tout fonction définie sur R, continue, telle que
Pour trouver le resultat général pour limite = l il suffit de poser g(x) = f(x) -lx
Mais comment montrer 1er resultat?
Relation limite
6 messages
- Page 1 sur 1
Relation limite
par savan-306D » 12 Nov 2014, 02:09
Salut,
J'ai croisé cette propriété, qui dit que tout fonction définie sur R, continue, telle que - f(x) = 0)
vérifie /x = 0)
Pour trouver le resultat général pour limite = l il suffit de poser g(x) = f(x) -lx
Mais comment montrer 1er resultat?
J'ai croisé cette propriété, qui dit que tout fonction définie sur R, continue, telle que
Pour trouver le resultat général pour limite = l il suffit de poser g(x) = f(x) -lx
Mais comment montrer 1er resultat?
par Ben314 » 12 Nov 2014, 10:10
Salut,
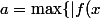Soit|\,;\,x\in[0,1]\})
(qui existe car 
est continue) et =f(x+1)-f(x)\)
.
On fixe
.
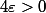
Comme=0)
, il existe 
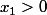
tel que |x_1)
on a :
|=|g(x-1)+g(x-2)+...+g(x-\lfloor x\rfloor)+f(x-\lfloor x\rfloor)|)
|+|g(x-2)|+...+|g(x-\lfloor x\rfloor)|+|f(x-\lfloor x\rfloor)|)
Comme
, parmi les 
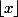
termes de la forme |)
, il y en a 
que l'on peut majorer par 
et les 
autres que l'on peut majorer par 
:
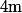
|\leq \lfloor x-x_1\rfloor\frac{\varepsilon}{2}+(\lfloor x\rfloor-\lfloor x-x_1\rfloor)m+a[\leq x\frac{\varepsilon}{2}+(x_1+1)m+a)
donc}{x}|\leq \frac{\varepsilon}{2}+\frac{(x_1+1)m+a}{x}\leq \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon)
à condition de prendre m+a}{\varepsilon/2})
Soit
On fixe
Comme
Comme
donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 12 Nov 2014, 12:58
Salut,
Soit et 
fixé.
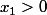
Comme, il existe tel que |x_1\)
, si 
on a 
donc
|\ =\ |g(x-1)+g(x-2)+...+g(x-k)+f(x-k)|)
|+|g(x-2)|+...+|g(x-k)|+|f(x-k)|)
donc}{x}\right|\leq \varepsilon+\frac{m}{x}\leq 2\varepsilon\)
à condition de prendre 
Soit
Comme
donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 12 Nov 2014, 13:07
Salut,
Soit et fixé.
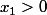
Comme, il existe tel que , si on a donc
donc à condition de prendre
Soit
Comme
donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :