Bonjour,
je suis ingénieur et j'ai à résoudre l'équation suivante :
h"(t) = a.h'(t) + Cste + b/h(t)
je connais les conditions aux limites h(t=0) et h'(t=0)
il y a bien longtemps (presque 20 ans), j'ai dû savoir résoudre ce type d'équation différentielle, mais malheureusement les maths ne sont pas comme le vélo, et j'ai bien peur d'être sérieusement rouillé.
Qui saurait m'aider ?
Par avance merci infiniment.
Nicolas
Resolution equation differentielle du type ah"+bh'+ch+d+e/h=0
8 messages
- Page 1 sur 1
bjr
je ne suis pas ingénieur, mais vais essayer de t'aider en attendant les cracks en maths
h"(t) = a.h'(t) + Cste + b/h(t)
je commence par resoudre l'equation generale
h"(t) = a.h'(t)
h"(t)/.h'(t) =a
integration donne
Ln(|h'(t)|)= at +cte
soit en passant par l'exponentielle
h'(t)= K.exp(at) +Cte
h(t)= k/a.exp(at) +Cte.t
ensuite tu fais varier la constante K
on derive la solution generale
h"(t) =dk.exp(at) +ak.exp(at) =dk.exp(at) +H'(t)= a.h'(t) + Cste + b/h(t)
soit dk.exp(at)= cte + b/h(t)
te laisse poursuivre..
je ne suis pas ingénieur, mais vais essayer de t'aider en attendant les cracks en maths
h"(t) = a.h'(t) + Cste + b/h(t)
je commence par resoudre l'equation generale
h"(t) = a.h'(t)
h"(t)/.h'(t) =a
integration donne
Ln(|h'(t)|)= at +cte
soit en passant par l'exponentielle
h'(t)= K.exp(at) +Cte
h(t)= k/a.exp(at) +Cte.t
ensuite tu fais varier la constante K
on derive la solution generale
h"(t) =dk.exp(at) +ak.exp(at) =dk.exp(at) +H'(t)= a.h'(t) + Cste + b/h(t)
soit dk.exp(at)= cte + b/h(t)
te laisse poursuivre..
C'est pas super dans mes cordes, mais il me semble me rappeler que, quand il n'y a "pas de x", du style :
=ay'(x)+\frac{b}{y(x)}+c)
tu as intérêt à "inverser", c'est à dire à chercher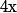 en fonction de
en fonction de 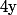 pour diminuer le degré de 1.
pour diminuer le degré de 1.
Ici, ça donne :
}{x'^3(y)}=\frac{a}{x'(y)}+\frac{b}{y}+c)
qui n'est plus qu'une équa. diff. du premier degré en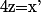 :
:
=-a z^2(y)-b\frac{z^3(y)}{y}-c z^3(y))
Mais quand à exprimer les solutions de façon simple...
tu as intérêt à "inverser", c'est à dire à chercher
Ici, ça donne :
qui n'est plus qu'une équa. diff. du premier degré en
Mais quand à exprimer les solutions de façon simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est pas super dans mes cordes, mais il me semble me rappeler que, quand il n'y a "pas de x", du style :
=ay'(x)+\frac{b}{y(x)}+c)
tu as intérêt à "inverser", c'est à dire à chercher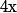 en fonction de
en fonction de 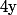 pour diminuer le degré de 1.
pour diminuer le degré de 1.
Ici, ça donne :
}{x'^3(y)}=\frac{a}{x'(y)}+\frac{b}{y}+c)
qui n'est plus qu'une équa. diff. du premier degré en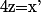 :
:
}{z^3(y)}=\frac{a}{z(y)}+\frac{b}{y}+c)
Mais quand à exprimer les solutions de façon simple...
tu as intérêt à "inverser", c'est à dire à chercher
Ici, ça donne :
qui n'est plus qu'une équa. diff. du premier degré en
Mais quand à exprimer les solutions de façon simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
On peut ramener à une équation du premier ordre ... Mais sa résolution reste hard
h"(t) = a.h'(t) + Cste + b/h(t)
Poser dh/dt = p
d²h/dt² = dp/dt = dp/dh * dh/dt = p.dp/dh
p.dp/dh = a.p + Cste + b/h
p.dp/dh - a.p = Cste + b/h
Equation du premier ordre non linéaire pas facile à résoudre ...
*****
Par contre, comme la question est posée par un ingénieur ...
Si on connait les valeurs numériques de a , de Cste , de b et celles de h(0) et h'(0), on peut résoudre numériquement (par exemple en utilisant Excel) et si on veut en sortir le graphe de h(t)
:zen:
h"(t) = a.h'(t) + Cste + b/h(t)
Poser dh/dt = p
d²h/dt² = dp/dt = dp/dh * dh/dt = p.dp/dh
p.dp/dh = a.p + Cste + b/h
p.dp/dh - a.p = Cste + b/h
Equation du premier ordre non linéaire pas facile à résoudre ...
*****
Par contre, comme la question est posée par un ingénieur ...
Si on connait les valeurs numériques de a , de Cste , de b et celles de h(0) et h'(0), on peut résoudre numériquement (par exemple en utilisant Excel) et si on veut en sortir le graphe de h(t)
:zen:
Ben314 a écrit:
Sauf erreur, c'est la même chose (avec p=1/z), ce qui n'est pas très surprenant...Black Jack a écrit:p.dp/dh - a.p = Cste + b/h
Quand on en sera aux problème de recollement des éventuelles solution, la question pourra... éventuellement se poser,mrif a écrit:Pour exprimer x en fonction de y il faut s'assurer que les solutions sont injectives!
Mais... on en est loin...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
