Montrer que Z_t est une martingale

[master-math]

Bonjour tous le monde,

J'ai un petit soucie, en fait je doit montrer que le processus est une martingale

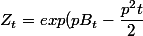
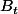
. Avec un mouvement Brownien de dim 1.

en fait j'ai introduit un et le s pour avoir le et je suis arrivée à une expression .

Je dois montrer que sachant que suit une loi normal de moyenne nulle et de variance (t-s). donc



après je vois pas trop comment continuer, pourriez vous m'aider svp! merci par avance

[SLA]

Bonjour tous le monde,

J'ai un petit soucie, en fait je doit montrer que le processus est une martingale

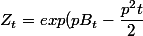
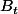
. Avec un mouvement Brownien de dim 1.

en fait j'ai introduit un et le s pour avoir le et je suis arrivée à une expression .

Je dois montrer que sachant que suit une loi normal de moyenne nulle et de variance (t-s). donc



après je vois pas trop comment continuer, pourriez vous m'aider svp! merci par avance

C'est bizarre que tu n'emploies pas une notation en espérance conditionelle...
ceci dit, tu as fait le plus dur, il te faut maintenant calculer cette intégrale pour conclure.

[master-math]

C'est bizarre que tu n'emploies pas une notation en espérance conditionelle...
ceci dit, tu as fait le plus dur, il te faut maintenant calculer cette intégrale pour conclure.

Vous avez raison, c'est des espérances conditionnelles. C'est bon, j'ai résout le problème