Convergence d'une suite dont les termes se rapprochent

[savan-306D]

Salut,
Si la limite
Est ce qu'on peut dire que Un converge?
Et merci d'avance

[barbu23]

Bonsoir,

Si , cela, à mon avis, n'implique pas que : , converge, car en général, on n'a que ça ( d'après une fameuse propriété du cours sur les séries numériques ) :
, mais pas : .
J'espère ne pas m'être trompé. :happy3:
Si je me suis trompé dans le raisonnement, vous me pardonnez. :happy3:

Cordialement. :happy3:

[mrif]

Non
essaie de regarder le comprtement de la suite

[Ben314]

Peut-être même avec la suite
(un peu plus compliqué pour trouver la limite de mais... bien moins compliqué pour trouver la limite de ...)

[savan-306D]

Ah je vois, l'énoncé original dit que si on a
avec
Alors converge.
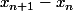
J'ai arrivé à montrer que tend vers 0. Mais là je bloque.
Si vous avez des pistes veuillez me les passer.

[Joker62]

Hello,

Montre déjà par récurrence que :

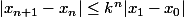
et après tu peux sommer pour n allant de 0 à m

[savan-306D]

Hello,

Montre déjà par récurrence que :

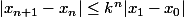
et après tu peux sommer pour n allant de 0 à m

La relation est facile à vérifier, après la somme j'ai obtenu en utilisant l'inégalité triangulaire :

Est ce que c'est le bon chemin ? Car là je ne vois pas comment déduire l'existence de la limite.

[Ben314]

Une première remarque : vu que 0
Sinon, j'ai l'impression que ton résultat est bon, mais tu n'en déduira pas grand chose : Il y a de forte chance que la suite n'ait pas comme limite son premier terme x0 donc ton truc ne tend pas vers 0 et ça ne va pas permettre d'en déduire que la limite existe (si par exemple |xn-5| reste majoré par 2, tu n'en déduit... pas grand chose à part que la suite est borné, mais on est loin du compte en ce qui concerne le fait qu'elle ait ou pas une limite)

Là, il te faut utiliser un outil un peu "puissant" : soit la notion de suites de Cauchy, soit le théorème qui dit que si une série est absolument C.V. alors elle est convergente : y'a pas un des deux que vous avez vu récemment en cours ?

[savan-306D]

Une première remarque : vu que 0<k<1 tu aurait intérêt à écrire plutôt des 1-k et 1-k^n (qui sont positifs) plutôt que leurs opposés : ça risque de t'éviter de faire des conneries (par exemple multiplier une inégalité par un négatif...)

Sinon, j'ai l'impression que ton résultat est bon, mais tu n'en déduira pas grand chose : Il y a de forte chance que la suite n'ait pas comme limite son premier terme x0 donc ton truc ne tend pas vers 0 et ça ne va pas permettre d'en déduire que la limite existe (si par exemple |xn-5| reste majoré par 2, tu n'en déduit... pas grand chose à part que la suite est borné, mais on est loin du compte en ce qui concerne le fait qu'elle ait ou pas une limite)

Là, il te faut utiliser un outil un peu "puissant" : soit la notion de suites de Cauchy, soit le théorème qui dit que si une série est absolument C.V. alors elle est convergente : y'a pas un des deux que vous avez vu récemment en cours ?

Je suis tout à fait d'accord, c'est la meme conclusion, pour les suites de cauchy, on n'a pas fait en cours ni la convergence absolue, or je sais la déf de suite de cauchy, et quelques propriétés, si t'as trouvé une solution grace à ce théorème, n'hésite pas à la poster.

[Ben314]

Tu fait exactement les mêmes calculs que ceux qui t'on conduit à ça :

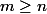
mais de façon à majorer à la place de (avec par exemple)
Et ta majoration te permettra de montrer que la suite est de Cauchy donc convergente.