Bonjour,
Je cherche à trouver la primitive de 1/(sqrt(x^2+1)).
La correction me dit que c'est Argsh(x) ou encore ln(x+sqrt(x^2+1)).
Je voudrais comprendre comment on trouve cette primitive, et aussi pourquoi Argsh(x)=ln(x+sqrt(x^2+1))?
Merci pour vos réponses.
Primitive
5 messages
- Page 1 sur 1
MC91 a écrit:Bonjour,
Je cherche à trouver la primitive de 1/(sqrt(x^2+1)).
La correction me dit que c'est Argsh(x) ou encore ln(x+sqrt(x^2+1)).
Je voudrais comprendre comment on trouve cette primitive, et aussi pourquoi Argsh(x)=ln(x+sqrt(x^2+1))?
Merci pour vos réponses.
bsr
tu poses :
x=Sh(u) donc u= argSh(x)
dx=Ch(u)du
puis tu sais que 1+Sh(u)² =Ch(u)²
1/(sqrt(x^2+1))dx = Ch(u)du/sqrt(1+Sh(u)²)
I= int(ch(u)/ch(u)du) = int(du)
on intègre I= u+Cte = argSh(x) +Cte
---------
exp(u)=Sh(u)+ Ch(u)
Ln(exp(u))= u =Ln[Sh(u) + ch(u)]=Ln[sh(u) +V(1+Sh(u)²) =u
tu poses x=Sh(u)
on a Ln [x+ V(1+x²)]= argSh(x)
salut
évidemment le changement de variable x = sh(t) convient ...
sinon http://www.ilemaths.net/forum-sujet-620885.html
....
évidemment le changement de variable x = sh(t) convient ...
sinon http://www.ilemaths.net/forum-sujet-620885.html
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Salut,
La fonction (ArgSinusHyperbolique) est la bijection réciproque de la fonction
(ArgSinusHyperbolique) est la bijection réciproque de la fonction 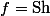 (SinusHyperbolique) qui est une bijection de R->R
(SinusHyperbolique) qui est une bijection de R->R
Donc, pour tout réel y,=\frac{1}{f'\circ f^{-1}(y)}=\frac{1}{\text{Ch}(\text{ArgSh}(y))}) .
.
Or, pour tout réel x,-\text{Sh}^2(x)=1) donc, comme
donc, comme \geq 0\) ,
, =\sqrt{\text{Sh}^2(x)+1}) d'où, en prenant
d'où, en prenant 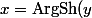) ,
, )=\sqrt{y^2+1}) ce qui donne le résultat.
ce qui donne le résultat.
Concernant la formule=\ln\big(y+\sqrt{y^2+1})) , elle découle du fait que, par définition,
, elle découle du fait que, par définition, 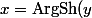) est la solution de l'équation (en x avec y fixé)
est la solution de l'équation (en x avec y fixé) =y\) c'est à dire
c'est à dire  que l'on résout simplement (équation du second degré) en posant
que l'on résout simplement (équation du second degré) en posant 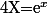 -> Fait le à titre d'exercice.
-> Fait le à titre d'exercice.
La fonction
Donc, pour tout réel y,
Or, pour tout réel x,
Concernant la formule
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
bonjour...réponse rapide...en générale pensez au changement de variable X=sinx ou cosx ...On a également recours à l'intégration par partie.
Voire également dérivées et intégrales sur internet avec des fonctions réciproques...
Evidemment il est indispensable de s'exercer à en retrouver les résultats...bon courage.
Voire également dérivées et intégrales sur internet avec des fonctions réciproques...
Evidemment il est indispensable de s'exercer à en retrouver les résultats...bon courage.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
