Merci d'avance :we:
Théorème encadrement et somme
8 messages
- Page 1 sur 1
Théorème encadrement et somme
Bonjour, je dois prouver par le théorème de l'encadrement que la suite ) définie par
définie par 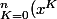/K!) tends vers
tends vers ) , or je ne sais pas comment commencer. Pouvez-vous me donner une indication ou l'inégalité de départ ?
, or je ne sais pas comment commencer. Pouvez-vous me donner une indication ou l'inégalité de départ ?
Merci d'avance :we:
Merci d'avance :we:
Salut,
As-tu vu une des "formules de Taylors" (avec reste intégral par exemple...) ?
Si oui, c'est le moment de t'en servir.
Si non, ça va être un peu long vu que, bon grès, mal grès, il va plus ou moins falloir la (re)démontrer dans ce cas particulier...
As-tu vu une des "formules de Taylors" (avec reste intégral par exemple...) ?
Si oui, c'est le moment de t'en servir.
Si non, ça va être un peu long vu que, bon grès, mal grès, il va plus ou moins falloir la (re)démontrer dans ce cas particulier...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Dans ce cas, c'est (quasiment) fini : Il suffit de montrer que la suite !}e^x) tend vers 0 pour conclure (à l'aide du théorème "des gendarmes")
tend vers 0 pour conclure (à l'aide du théorème "des gendarmes")
Pour ce faire, je t'inciterais bien à commencer par calculer la limite de dans le but de majorer la suite
dans le but de majorer la suite _{n\geq 0}) par une suite géométrique de raison
par une suite géométrique de raison  .
.
Pour ce faire, je t'inciterais bien à commencer par calculer la limite de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, c'est juste.nicolas2 a écrit:J'ai trouvé, est-ce juste ? Et je n'ai pas compris comment transposer cela en une suite géométrique ?
Et cette quantité tend clairement vers 0 lorsque n tend vers +oo ce qui signifie (par définition d'une limite) qu'il existe un certain entier m tel que
Donc
et, de façon générale, pour tout k on a
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
