Involution
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
glouglu
- Membre Naturel
- Messages: 19
- Enregistré le: 24 Sep 2014, 16:20
-
 par glouglu » 03 Nov 2014, 17:34
par glouglu » 03 Nov 2014, 17:34
Bonjour,
J'ai un problème sur un exercice concernant les involutions.
Soit E un espace vectoriel sur C;
On sait que si A est un endomorphisme , nous posons
= \{ x \in E / A(x)=x \})
et
= \{ A(x)-x / x \in E\})
. F(A) et G(A) sont 2 sous espaces vectoriels.
On doit prouver que
= \{ i(x)+x / x \in E\})
et
= \{x \in E / i(x)=-x\})
tel que
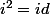
(involution)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Nov 2014, 20:00
par zygomatique » 03 Nov 2014, 20:00
salut
énoncé incompréhensible ....
a ?
E ?
i ?
la deuxième phrase n'en est pas une (il n'y a pas de verbe dans ce qui suit la virgule)
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
glouglu
- Membre Naturel
- Messages: 19
- Enregistré le: 24 Sep 2014, 16:20
-
 par glouglu » 03 Nov 2014, 20:08
par glouglu » 03 Nov 2014, 20:08
zygomatique a écrit:salut
énoncé incompréhensible ....
a ?
E ?
i ?
la deuxième phrase n'en est pas une (il n'y a pas de verbe dans ce qui suit la virgule)
...
J'ai édité :we:

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Nov 2014, 20:58
par zygomatique » 03 Nov 2014, 20:58
ben il est évident que
i(i(x) + x) = x + i(x) donc si u = i(x) + x on a i(u) = u
et
i(i(x) - x) = x - i(x) donc si v = i(x) - x alors i(v) = -v
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
glouglu
- Membre Naturel
- Messages: 19
- Enregistré le: 24 Sep 2014, 16:20
-
 par glouglu » 04 Nov 2014, 17:14
par glouglu » 04 Nov 2014, 17:14
zygomatique a écrit:ben il est évident que
i(i(x) + x) = x + i(x) donc si u = i(x) + x on a i(u) = u
et
i(i(x) - x) = x - i(x) donc si v = i(x) - x alors i(v) = -v
...
Merci :we:
Je me pose la question si F et G sont supplémentaires.
l'intersection est vide mais je n'arrive pas à montrer que F+G=E...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Nov 2014, 17:16
par Ben314 » 04 Nov 2014, 17:16
glouglu a écrit:l'intersection est vide mais je n'arrive pas à montrer que F+G=E...
L'intersection de deux sous espaces vectoriels ne peut
JAMAIS être vide vu que tout sous espace vectoriel contient le vecteur nul.
Sinon, tout
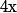
de E s'écrit
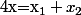
où
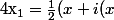)\in F)
et
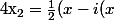)\in G)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités