Problème dérivée fonction

[Annarose]

Bonjour,

Je bloque sur une question issue d'un devoir maison.

Soit la fonction f définie sur [1/2 ; 2 ] avec f(x)= -3x + 5 - 3/2x^2

Je dois déterminer la fonction dérivée f'(x) et la mettre sous la forme d'un quotient.

Pour le début ça va:
-3x donne -3
5 donne 0

Mais je bloque avec la division.
Je ne sais pas si la dérivée de 3/2x^2 c'est:

3/2 * -1/(x^2)^2

Ou alors 6 / 2x^3

Ou encore -6 / 6x^3


Mais peut-être que je me plante complètement, donc si quelqu'un peut m'aider ce serait génial, merci beaucoup!

[Fred_Sabonnères]

Bonsoir


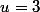
avec donc

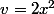
et donc

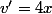
Il n'y a plus qu'à appliquer :ptdr:

[Annarose]

Ce qui ferait -12x / 2x^4 ?

[WillyCagnes]

bsr

(3/2)/x² =(3/2).(x-²)

la derivée = -2(3/2).x-(2+1)
= -3.x^-3
=-3/x^3

[Annarose]

Du coup pour la dérivée complète de f(x)= -3x + 5 - 3/2x^2 ça donne:

f'(x)= -3 + 12x / 2x^4

C'est ça?
Parce qu'il est demandé de la mettre sous la forme d'un quotient?

[WillyCagnes]

tu t'es trompe pour v²=(2x²)=4x^4

plutot
F'(x)= -3 +3/x^3

s'annule pour x=1

[Annarose]

Je ne comprends pas la dérivée = -2(3/2).x-(2+1)

[WillyCagnes]

U= x^n
u'= n.x^(n-1)

si n=-2
U'=-2x^(-2-1)
U'=-2x^-3 tout simplement

puis si on le multiplie par -3/2
U'= +3.x^-3 = 3/x^3

plus facile à deriver x^(-2) que 1/x² avec la forme (u'v-v'u)/v², la preuve tu t'etais trompé dans le v²=4x² au lieu de ton 2x²

[Fred_Sabonnères]

Bonjour
Pour ne pas avoir d'erreur, c'est quand même mieux d'écrire en Latex.
Ta fonction est:


Ta dérivée est donc:


Et tu vois de suite pour quelles valeurs de x ta fonction dérivée s'annule :ptdr:

[Annarose]

(Je ne sais pas comment écrire en Latex :S )

Elle s'annule? C'est-à-dire? On retrouve le x^3 en haut et en bas de la fraction ok mais...?

[Fred_Sabonnères]

On voit que x=1 est solution. Reste à savoir s'il y a d'autres valeurs de x qui annulent le numérateur :lol3:

[Annarose]

Ok, j'ai réussi à terminer mon exercice. Merci beaucoup! :)