Complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anne33
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Oct 2014, 14:16
-
 par Anne33 » 29 Oct 2014, 14:26
par Anne33 » 29 Oct 2014, 14:26
J'ai un DM à rendre à la rentré et l'on me demande de résoudre z^2-(2^(téta+1)cos téta)z+2^(2téta)=0. Avec téta compris entre ]0;2pi[
J'ai calculé delta : 2^(2téta +1) cos 2téta -8^(2téta).
Je ne suis pas sur de mon résultat et je ne sais pas quoi faire après.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Oct 2014, 14:49
par chan79 » 29 Oct 2014, 14:49
Anne33 a écrit:J'ai un DM à rendre à la rentré et l'on me demande de résoudre z^2-(2^(téta+1)cos téta)z+2^(2téta).
J'ai calculé delta : 2^(2téta +1) cos 2téta -8^(2téta).
Je ne suis pas sur de mon résultat et je ne sais pas quoi faire après.
salut
tu devrais arriver à
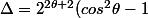)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Oct 2014, 15:13
par barbu23 » 29 Oct 2014, 15:13
Bonjour,
On peut aussi procéder ainsi :
 z + 2^{ 2 \theta } = z^{2} - 2 \times 2^{ \theta } \cos ( \theta ) + ( 2^{ \theta } )^2)
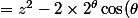 z + [( 2^{ \theta} )^2 \times 1])
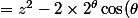 z + [( 2^{ \theta} )^2 \times ( \cos^2 ( \theta ) + \sin^2 ( \theta ) )])
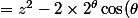 z + [( 2^{ \theta} )^2 \cos^2 ( \theta ) ]+ [ ( 2^{ \theta } )^2 \sin^2 ( \theta ) )])
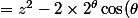 z + ( 2^{ \theta} \times \cos ( \theta ) )^2 + ( 2^{ \theta } \sin ( \theta ) )^2)
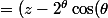)^2 + ( 2^{ \theta } \sin ( \theta ) )^2)
A toi de finir la factorisation. :happy3:
Cordialement. :happy3:
-
Anne33
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Oct 2014, 14:16
-
 par Anne33 » 29 Oct 2014, 21:05
par Anne33 » 29 Oct 2014, 21:05
chan79 a écrit:salut
tu devrais arriver à
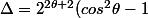)
Merci bcp mais je ne sais pas comment arriver a ce résultat car delta= b^2-4ac et je ne comprends pas où est passé le 4ac?
-
Anne33
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Oct 2014, 14:16
-
 par Anne33 » 30 Oct 2014, 11:05
par Anne33 » 30 Oct 2014, 11:05
barbu23 a écrit:Bonjour,
On peut aussi procéder ainsi :
 z + 2^{ 2 \theta } = z^{2} - 2 \times 2^{ \theta } \cos ( \theta ) + ( 2^{ \theta } )^2)
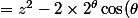 z + [( 2^{ \theta} )^2 \times 1])
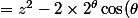 z + [( 2^{ \theta} )^2 \times ( \cos^2 ( \theta ) + \sin^2 ( \theta ) )])
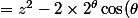 z + [( 2^{ \theta} )^2 \cos^2 ( \theta ) ]+ [ ( 2^{ \theta } )^2 \sin^2 ( \theta ) )])
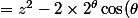 z + ( 2^{ \theta} \times \cos ( \theta ) )^2 + ( 2^{ \theta } \sin ( \theta ) )^2)
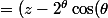)^2 + ( 2^{ \theta } \sin ( \theta ) )^2)
A toi de finir la factorisation. :happy3:
Cordialement. :happy3:
Merci beaucoup mais je dois résoudre l'équation égale à zéro.
-
Anne33
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Oct 2014, 14:16
-
 par Anne33 » 30 Oct 2014, 11:14
par Anne33 » 30 Oct 2014, 11:14
chan79 a écrit: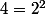
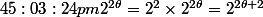
Merci je comprends maintenant. Désoler de vous embêter encore:
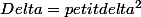
et je voudrai savoir comment trouver petit delta afin de calculer les racines.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Oct 2014, 18:28
par chan79 » 30 Oct 2014, 18:28
Anne33 a écrit:Merci je comprends maintenant. Désoler de vous embêter encore:
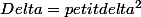
et je voudrai savoir comment trouver petit delta afin de calculer les racines.
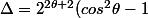=((2^{\theta +1}\times i \,sin \theta)^2)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Oct 2014, 18:38
par barbu23 » 30 Oct 2014, 18:38
Anne33 a écrit:Merci beaucoup mais je dois résoudre l'équation égale à zéro.
Tu appliques l'identité :
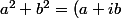(a - ib ))
et le fait qu'en général :
(x-b) = 0)
implique que :
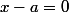
ou
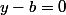
.
Cordialement. :happy3:
-
Anne33
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Oct 2014, 14:16
-
 par Anne33 » 30 Oct 2014, 19:09
par Anne33 » 30 Oct 2014, 19:09
chan79 a écrit: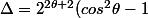=((2^{\theta +1}\times i \,sin \theta)^2)
Merci. j'ai calculé les racines et je trouve:
z1=
) /2)
z2=
) /2)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Oct 2014, 20:28
par chan79 » 30 Oct 2014, 20:28
Anne33 a écrit:Merci. j'ai calculé les racines et je trouve:
z1=
) /2)
z2=
) /2)
oui
plus simplement

et
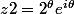
on vérifie facilement la somme et le produit des racines
-
Anne33
- Membre Naturel
- Messages: 20
- Enregistré le: 29 Oct 2014, 14:16
-
 par Anne33 » 31 Oct 2014, 10:39
par Anne33 » 31 Oct 2014, 10:39
D'accord je comprends merci beaucoup à vous deux.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
