Des fonctions dans un triangle

[Yaya18]

Bonsoir, récemment j'ai eu un DM de maths mais je ne suis pas sûr de mes réponses et si quelqu'un pourrait me corriger ce serait parfait ! :we:

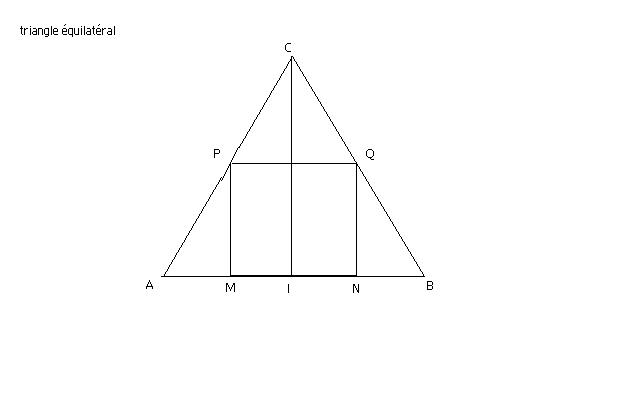
f est la fonction qui a x= AM associe en cm² l'aire du rectangle MNQP
a) Quel est l'ensemble des définition de f
b) Exprimer MN puis MP en fonction de x et en déduire l'expression algébrique
c) Calculer f(3) puis verifier que pour tous x de [0;6] : f(x)-f(3)=-2V3 (x-3)²
d) En déduire que f(3) est le maximum de f sur [0;6]
e) Quelles sont les dimensions du rectangle d'aire maximale ?


Voici mes réponses :

a) x = AM, M appartient [AI] et AI=6 cm, donc 0 (ou égale) 0 (un carré est toujours positif)
-2(racine)3 (x-3) au carré <(ou égale) 0
donc f(x) - f(3) <(ou égale) 0 et f(x) <(ou égale) f(3) et f(3) est le maximum.

e) Le maximum est atteint pour x =3
Les dimensions du rectangle d'aire maximale sont :
MN = 12-2*3 =6
MP = 3V3

Merci pour ceux qui prendront la peine de me répondre

[gigamesh]

Pas d'erreur. Exercice bien traité.
(A part le 3=PM/x qui devrait être racine(3)=PM/x mais à la ligne d'après tu as bien écrit PM=racine(3)*x )

[Yaya18]

Pas d'erreur. Exercice bien traité.
(A part le 3=PM/x qui devrait être racine(3)=PM/x mais à la ligne d'après tu as bien écrit PM=racine(3)*x )

Merci beaucoup, je corrigerai la faute C'était sans doute une erreur de frappe

[gigamesh]

Merci beaucoup, je corrigerai la faute C'était sans doute une erreur de frappe

Oui, manifestement tu avais seulement oublié d'écrire le "racine".