Démontrer par récurrence un produit
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pommedepin
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Oct 2014, 16:24
-
 par Pommedepin » 28 Oct 2014, 10:18
par Pommedepin » 28 Oct 2014, 10:18
Hello !
J'ai une récurrence à démontrer, mais je ne sais pas du tout comment m'y prendre... Cela part d'une notation que je n'ai encore jamais utilisée en récurrence du moins...
Voilà ce que je dois montrer :
"Pour tout entier" n appartenant à N, produit de k=0 jusqu'à n (2k+1) = (2n+1)!/(2^n)n!
Je dois ici impérativement utiliser une récurrence, je suis bloquée à l'hérédité.
Merci d'avance
-
Pommedepin
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Oct 2014, 16:24
-
 par Pommedepin » 28 Oct 2014, 10:56
par Pommedepin » 28 Oct 2014, 10:56
Juste un update.
-
Pommedepin
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Oct 2014, 16:24
-
 par Pommedepin » 28 Oct 2014, 11:26
par Pommedepin » 28 Oct 2014, 11:26
Juste pour updater le message =)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Oct 2014, 11:56
par chan79 » 28 Oct 2014, 11:56
salut
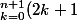=(2n+3)\bigprod_{k=0}^{n}(2k+1)=\fra{(2n+3)(2n+1)!}{2^n n!})
ensuite tu as juste à remarquer que
(2n+1)!=\fra{(2n+3)!}{2n+2})
-
Pommedepin
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Oct 2014, 16:24
-
 par Pommedepin » 28 Oct 2014, 12:30
par Pommedepin » 28 Oct 2014, 12:30
Merci de votre réponse !
Je ne comprends pas d'où vient le (2n+3)... Je comprends pas la suite non plus d'ailleurs. En quoi remarquer ça : (2n+3)(2n+1)!=\fra{(2n+3)!}{2n+2}
peut m'ammener à ça : (2n+1)!/(2^n)n! ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Oct 2014, 12:44
par chan79 » 28 Oct 2014, 12:44
Pommedepin a écrit:Merci de votre réponse !
Je ne comprends pas d'où vient le (2n+3)... Je comprends pas la suite non plus d'ailleurs. En quoi remarquer ça : (2n+3)(2n+1)!=\fra{(2n+3)!}{2n+2}
peut m'ammener à ça : (2n+1)!/(2^n)n! ?
!=(2n+3)(2n+2)(2n+1)!)
donc, tu peux remplacer
(2n+1)!)
par
!}{2n+2})
soit
!}{2(n+1)})
-
Pommedepin
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Oct 2014, 16:24
-
 par Pommedepin » 28 Oct 2014, 13:18
par Pommedepin » 28 Oct 2014, 13:18
Mais d'où vient ce 2n+3 ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Oct 2014, 14:09
par chan79 » 28 Oct 2014, 14:09
Pommedepin a écrit:Mais d'où vient ce 2n+3 ?
pour k=n+1, 2k+1=2n+3
-
Pommedepin
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Oct 2014, 16:24
-
 par Pommedepin » 28 Oct 2014, 14:33
par Pommedepin » 28 Oct 2014, 14:33
Exact ! Je comprends mieux maintenant, merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
