Raisonnement par récurrence

[Pommedepin]

Bonjour à tous :)

J'ai une démonstration par récurrence à faire et arrivée à l'hérédité, j'ai beaucoup de mal.... Je dois en fait démontrer que ((x+1)(x+4))/(4(x+2)(x+3)) = (x(x+3)²+4)/(4(x+1)(x+2)(x+3))...

Je pense savoir que les deux sont effectivement équivalentes car leur représentation graphique est la même... Pour le démontrer je suis perdue. :mur:

Merci d'avance

[barbu23]

Salut : :happy3:

D'abord, je ne sais pas si et un entier naturel ou bien un réel. Ensuite, si on suppose que c'est un entier naturel, l'égalité ne s'établit pas par récurrence, mais par une suite d'égalité, en partant de l'un des membres pour arriver à l'autre membre de l'égalité. Si tu optes pour la récurrence pour établir ton égalité, c'est un peu long et rébarbatif, et inutile il me semble. Bon, c'est juste un conseil. Libre à toi de choisir la méthode qui te convient.
Par contre, si est un réel, on n'applique jamais une récurrence pour établir ta formule. :happy3:
La récurrence est conçu pour établir des formules dans seulement, et pas dans par exemple. :happy3:

Cordialement. :happy3:

[Pommedepin]

Bonjour ! Tout d'abord, merci pour votre réponse !
Alors oui, x appartient à N, pardon de ne pas l'avoir spécifié.

Ensuite, ce que je dois démontrer par récurrence c'est

Somme pour k=1 allant jusqu'à n de 1/(k(k+1)(k+2)) = (n(n+3))/(4(n+1)(n+2)) d'où l'utilisation d'une récurrence.

J'ai obtenu cette formule [((x+1)(x+4))/(4(x+2)(x+3)) = (x(x+3)²+4)/(4(x+1)(x+2)(x+3))] à l'hérédité en utilisant mon hypothèse de récurrence. En effet après cela, je comptais utiliser une suite d'égalité, mais je suis bloquée...

[barbu23]

Bonjour, :happy3:

A mon avis, il serait préférable de décomposer en une somme de fractions simples pour pouvoir calculer : par simplification des additions.
Autrement dit, il fut faire une décomposition en éléments simples comme suit :
Il faut trouver :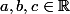 tels que : . C'est facile ainsi, au lieu d'opter pour une récurrence. :happy3:

Cordialement. :happy3:

[Ben314]

Salut,
Et si tu exprimait les deux truc avec le même dénominateur et que tu développe ensuite les deux numérateurs (pour voir s'ils sont égaux ou pas), ça ferait quoi ?

[Pommedepin]

Le fait de démontrer par récurrence est en fait dit dans l'énoncé... Mon prof ne me laisse pas vraiment le choix sur la méthode à adopter ^^

Ah et n est un entier naturel non nul du coup...

Merci =)

[Pommedepin]

Salut,
Et si tu exprimait les deux truc avec le même dénominateur et que tu développe ensuite les deux numérateurs (pour voir s'ils sont égaux ou pas), ça ferait quoi ?

Bonjour Ben !
J'ai essayé, à gauche ça me donne au numérateur : n²+5n+4 et à droite au numérateur ça me donne : n^3+6n²+9n+4

[Pommedepin]

Salut,
Et si tu exprimait les deux truc avec le même dénominateur et que tu développe ensuite les deux numérateurs (pour voir s'ils sont égaux ou pas), ça ferait quoi ?

ça me donne exactement le bon résultat...

Merci beaucoup, vraiment !

[barbu23]

Dur dur ... Ton prof semble être un vrai bourreau. :ptdr:

[Pythales]

Le fait de démontrer par récurrence est en fait dit dans l'énoncé... Mon prof ne me laisse pas vraiment le choix sur la méthode à adopter ^^

Ah et n est un entier naturel non nul du coup...

Merci =)

Si je peux me permettre d'intervenir ...
En fait, il faut montrer que
Après une mise en facteur, le calcul vise a montrer que
ce qui est élémentaire ...

[Ben314]

A mon avis, il serait préférable de décomposer en une somme de fractions simples pour pouvoir calculer : par simplification des additions.
Autrement dit, il fut faire une décomposition en éléments simples comme suit :
Il faut trouver : tels que : . C'est facile ainsi, au lieu d'opter pour une récurrence.

SUPER IDEE... :triste: :triste: :triste:
Dis, barbu, dans le cas d'une fraction "super simple", par exemple 1/k, tu peut me dire combien ça fait exactement s'il te plait ?

[barbu23]

SUPER IDEE... :triste: :triste: :triste:
Dis, barbu, dans le cas d'une fraction "super simple", par exemple 1/k, tu peut me dire combien ça fait exactement s'il te plait ?

Non, je voulais dire qu'il y'aurait probablement des simlifiction additionnelle de type : . Juste à titre d'exemple. :happy3: Je l'ai pas encore testé. Tu l'as testé toi et ça n'a pas marché ? :happy3: