EX de Suite raisonnement par récurence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
arso02100
- Messages: 4
- Enregistré le: 27 Oct 2014, 14:44
-
 par arso02100 » 27 Oct 2014, 15:05
par arso02100 » 27 Oct 2014, 15:05
Bonjour à tous
Voici l'énoncé
Exercice 1 : On considère la suite dé;)nie par :
Un+1 = (n+Un)/n²
U1=1 1. Montrer que Un  2, Pour tout n>1. INITIALISATION
2, Pour tout n>1. INITIALISATION vérifions que P(1) est vraie pour tout n>1
On a u1=1 donc 1;)2
HEREDITE supposons que P(n) est vraie pour tout n1 N et que P(n+1) soit vraie
Un+1 HEREDITE
supposons que P(n) est vraie pour tout n1 N et que P(n+1) soit vraie
Un+1

2
Un;)2
n+un

2+n
(n+Un)/n²

2+n/n²

2
je suis bloqué après je sais pas quoi faire je pige rien[U]
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 27 Oct 2014, 15:31
par annick » 27 Oct 2014, 15:31
Bonjour,
je crois que tu as sensiblement fini.
Tu as écrit : (n+Un)/n² ;) 2+n/n² ;) 2 , ce qui veut dire que Un+1<=2
Donc ta proposition est vraie pour U1, pour Un et pour Un+1, donc elle est toujours vraie.
Et tu as fini ta démonstration :lol3:
-
mathelot
 par mathelot » 27 Oct 2014, 15:34
par mathelot » 27 Oct 2014, 15:34
regardons
héréditaire , si

si

vrai, si

vrai, si
^2 \geq 17/4)
vrai, si

vrai, si

vrai, si
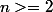
-
arso02100
- Messages: 4
- Enregistré le: 27 Oct 2014, 14:44
-
 par arso02100 » 27 Oct 2014, 15:38
par arso02100 » 27 Oct 2014, 15:38
annick a écrit:Bonjour,
je crois que tu as sensiblement fini.
Tu as écrit : (n+Un)/n²

2+n/n²

2 , ce qui veut dire que Un+1<=2
Donc ta proposition est vraie pour U1, pour Un et pour Un+1, donc elle est toujours vraie.
Et tu as fini ta démonstration :lol3:
Faut il le montrer pour tout n;)2 puisque pour n=1 la propriété est vérifiée.
Comment faire pour le prouver ?
Merci
-
arso02100
- Messages: 4
- Enregistré le: 27 Oct 2014, 14:44
-
 par arso02100 » 27 Oct 2014, 15:48
par arso02100 » 27 Oct 2014, 15:48
mathelot a écrit:regardons
héréditaire , si

si

vrai, si

vrai, si
^2 \geq 17/4)
vrai, si

vrai, si

vrai, si
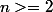
Merci pour les infos mais je comprend pas de ou viens ce 2n² quel est votre méthode? je débute dans les suite et j'ai pas d'exercice similaire pour comparer
Cordialement
-
mathelot
 par mathelot » 27 Oct 2014, 15:56
par mathelot » 27 Oct 2014, 15:56
euh, dsl.
On souhaite obtenir
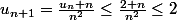
la 1ère inégalité est vraie, suite à l'hypothèse de récurrence.
La seconde inégalité est vraie pour

comme on désire sa véracité, on procède par condition
suffisante(pas forcément nécessaire) pour obtenir

(1). (1) est vraie par transitivité si
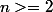
-
mathelot
 par mathelot » 27 Oct 2014, 16:04
par mathelot » 27 Oct 2014, 16:04
exemple de condition suffisanteon veut montrer que

tend vers l'infini avec

or
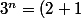^n \geq 2n+1)
par le développement du binome.
Si on veut que

dépasse tout nombre A>0 fixé

il suffit que

mais ce n'est pas nécessaire
-
arso02100
- Messages: 4
- Enregistré le: 27 Oct 2014, 14:44
-
 par arso02100 » 27 Oct 2014, 16:47
par arso02100 » 27 Oct 2014, 16:47
mathelot a écrit:exemple de condition suffisanteon veut montrer que

tend vers l'infini avec

or
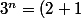^n \geq 2n+1)
par le développement du binome.
Si on veut que

dépasse tout nombre A>0 fixé

il suffit que

mais ce n'est pas nécessaire
Merci pour les infos c'est la premiere fois que j'entend parler de transitivité et de condition sufisante! lol si mon developement est bon ainsi ca sera déjà pas mal mais je vais me renseigner sur cette technique.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
