Bonjour, j'aimerais avoir une aide pour cet exercice car je bloque :
On considère deux urnes U et V contenant respectivement trois boules numérotées 0 et trois boules numérotées 1. On appelle échange l'épreuve consistant à tirer une boule de U et une boule de V puis à les échanger (mettre chaque boule tirée dans l'urne dont elle ne provient pas). Pour tout n entier naturel, on désigne par X_n la variable aléatoire donnant la somme des numéros inscrits sur les boules se trouvant dans l'urne U à l'issue des n échanges.
a) Exprimer chacune des probabilités P(X_(n+1)=0) , P(X_(n+1)=1), P(X_(n+1)=2) et P(X_(n+1)=3) en fonction de P(X_n=0), P(X_n=1), P(X_n=2) et P(X_n=3).
L'exercice continu mais avant de le poster, j'aimerais réussir cette première question pour débloquer la suite.
j'ai écrit :
P(X_(n+1)=0)=P(X_(n+1)=0/X_n=0)P(X_n=0)
P(X_(n+1)=1)=P(X_(n+1)=1/X_n=1)P(X_n=1)
P(X_(n+1)=2)=P(X_(n+1)=2/X_n=2)P(X_n=2)+P(X_(n+1)=2)P(X_n=1)P(X_n=1)
bon je pense que c'est faux car j'ai du mal à comprendre comment faire
merci de m'aider !
Probabilité
11 messages
- Page 1 sur 1
en effet, ce que tu a écrit est faux car:
P(X_n=0) \neq P(X_{n+1} = 0))
en réalité:
P(X_n=0) = P(X_{n+1} = 0 et X_n =0))
car pour des événements A et B:
P(B) = P(A et B))
Ce que tu devrais utiliser est la formule des probabilités totales:
[url=http://fr.wikipedia.org/wiki/Formule_des_probabilités_totales]lien[/url]
qui te donnera:
 = P(X_{n+1}=0|X_n=0)P(X_n=0) \\ + P(X_{n+1}=0|X_n=1)P(X_n=1) \\ +P(X_{n+1}=0|X_n=2)P(X_n=2)\\+P(X_{n+1}=0|X_n=3)P(X_n=3))
ensuite tu raisonnes avec la structure du problème pour déterminer ces 4 probabilités conditionelles.
Par ex:
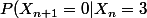 = 0) car une étape n'échange qu'une seule boule donc il est impossible de passer de 3 boules numérotés '1' à zéro boules numérotés '1' en une étape.
car une étape n'échange qu'une seule boule donc il est impossible de passer de 3 boules numérotés '1' à zéro boules numérotés '1' en une étape.
voila, j'espère que cela te met sur la bonne piste.
en réalité:
car pour des événements A et B:
Ce que tu devrais utiliser est la formule des probabilités totales:
[url=http://fr.wikipedia.org/wiki/Formule_des_probabilités_totales]lien[/url]
qui te donnera:
ensuite tu raisonnes avec la structure du problème pour déterminer ces 4 probabilités conditionelles.
Par ex:
voila, j'espère que cela te met sur la bonne piste.
pluie2 a écrit:ok merci je vais essayer de chercher et si j'ai un problème je vous dis ça d'ici à demain
par contre :
pour le reste des probabilités, dois je faire le meme calcul ? (pour le P(X_(n+1)=1) par exemple?
Oui : tu as 4 calculs à faire pour chaque P(X_(n+1)=?) avec ?=0,1,2,3
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
pluie2 a écrit:d'accord donc admettons prenons :
P(X_(n+1)=0/X_n=1)= proba qu'au bout de n+1 échanges, la somme dans U1 soit égale à 0 sachant qu'on avait 1 auparavant. Donc on a retiré de U1 la boule n°1 et celle n°0 dans U2. Donc P()=1/3*1/3 ?
Oui, c'est bien ça.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
pluie2 a écrit:d'accord donc pour la suite :
P(X_(n+1)=0/X_n=2)=proba qu'au bout de n+1 échanges, la somme dans U1 soit égale à 0 sachant qu'avant, elle était de 2. elle vaut 0 cette probabilité non ?
Oui et de façon un peu plus générale, P(X_{n+1}=a|X_n=b)=0 lorsque a et b diffèrent de strictement plus d'une unité.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Le vecteur ligne (0 1 2 3) fois le vecteur colonne
Et comme
Aprés, si on veut une expression précise de ça, je pense qu'il faut calculer
A moins qu'il n'y ait une astuce qui m'échape...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
