Limite d'une racine n-ième

par **Aubenoire** » 23 Oct 2014, 15:37

Bonjour !
J'ai un problème de limite, il n'est sûrement pas si difficile mais je ne sais plus comment faire :help: . La limite à calculer est la suivante :

lim(n-->+inf) An = lim (n-->+inf) (3^n + 4^n + 5^n)^(1/n).

Est-ce qu'il faut utiliser les logarithmes ? Ou le théorème du sandwich (ça se dit aussi comme ça en français ? désolé si le terme est incorrect, j'étudie en Suisse allemande) peut-être ?

Merci d'avance à la brave âme qui m'aidera :ptdr: !

(Et excusez-moi si je ne réponds pas rapidement, mon réseau a du mal ce soir, ou encore, si j'ai posté à la mauvaise place)

par **arnaud32** » 23 Oct 2014, 16:06

par **barbu23** » 23 Oct 2014, 16:08

Bonjour, :happy3:

Sauf erreur :

.

Essayes de finir seul le développement de cette expression. :happy3:

Cordialement. :happy3:

Edit : Grillé. :hum:

par **Aubenoire** » 23 Oct 2014, 18:49

Alors merci Arnaud, même si je t'avoue que ça ne m'aide que moyennement car je ne sais pas du tout quoi faire des logarithmes :hein:

Merci monsieur le barbu, je vais tenter de creuser là-dessus, et si je désespère vraiment je reviendrai abuser de la sagesse des internautes

Edit : Monsieur le barbu, vous êtes mon héros ! :ptdr: Merci beaucoup !

par **mathelot** » 23 Oct 2014, 20:06

Aubenoire a écrit: ça ne m'aide que moyennement car je ne sais pas du tout quoi faire des logarithmes

bonsoir,

on sait que

Le 1er facteur a pour limite 5.

Pour le second facteur, ça donne une expression de la forme

,

u tendant très rapidement vers zéro.

remarque

en France , nous disons "théorème des gendarmes" plutôt que "théorème du sandwich".

:petard:

par **Aubenoire** » 23 Oct 2014, 22:01

Merci Mathelot, c'est déjà plus clair !

Par contre, lorsque tu écris :
ln(1+h) = h + o(h),
o(h), c'est une fonction linéaire ?

(c'est de la simple curiosité, j'ai déjà calculé la limite, mais bon, j'en ai encore toute une série, alors autant être au taquet^^)

par **mathelot** » 23 Oct 2014, 22:34

Il y a quelque notations que je connais mal, dite de Landau

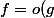au voisinage de

s'il existe un voisinage de

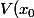, pour tout

où

et

reporte toi au Wiki "notation de Landau".

Aubenoire a écrit:Par contre, lorsque tu écris :
ln(1+h) = h + o(h),
o(h), c'est une fonction linéaire ?

au mieux, quadratique.

exemples de o(h):

Limite d'une racine n-ième

Limite d'une racine n-ième

Qui est en ligne