Faisceau

[barbu23]

Bonsoir à tous,

Est ce qu'il existe un faisceau dont les sections sont des polynômes définis sur des ouverts d'une topologie. Si oui, quelle est cette topologie. Est ce que c'est la topologie de Zariski, et pourquoi ? Et comment note-t-on ce faisceau ?. et est ce que les fermés de la topologie de Zariski peuvent être des ouverts sur quels sont définis ces polynômes ? Si la réponse est non, pourquoi on ne munit pas un faisceau d'une topologie de fermes au lieu d'ouverts sur quels sont définies les sections ?

Merci d'avance.

[L.A.]

Bonsoir,

Prenons n'importe quel espace topologique irréductible, et munissons le du faisceau F défini par F(U)=A où A est un anneau de polynôme fixé, et la restriction F(U) -> F(V) est l'identité. Alors F est un faisceau dont les sections sont des polynômes, mais l'espace est quelconque et n'a rien à voir a priori avec la topologie de Zariski.

Je sais pas si je réponds exactement à ta question, peut-être que tu peux l'affiner si ce n'est pas le cas...

Définir un faisceau sur les fermés, je ne crois pas que ça soit très adapté vis à vis des histoires de recollement de sections (puisque une réunion de fermés n'est pas fermée en général). Du coup, à quoi bon ?

[barbu23]

Bonsoir,

Prenons n'importe quel espace topologique irréductible, et munissons le du faisceau F défini par F(U)=A où A est un anneau de polynôme fixé, et la restriction F(U) -> F(V) est l'identité. Alors F est un faisceau dont les sections sont des polynômes, mais l'espace est quelconque et n'a rien à voir a priori avec la topologie de Zariski.

Je sais pas si je réponds exactement à ta question, peut-être que tu peux l'affiner si ce n'est pas le cas...

Définir un faisceau sur les fermés, je ne crois pas que ça soit très adapté vis à vis des histoires de recollement de sections (puisque une réunion de fermés n'est pas fermée en général). Du coup, à quoi bon ?

Merci pour ta réponse.
Il me semble que ton faisceau est défini par : avec un ouvert d'un espace toplogique , ou peut être c'est un faisceau constant, comme suit : pour tout , non ?
Moi, je veux définir un faisceau de la manière suivante : , je ne sais pas s'il est légitime d'écrire comme ça ? Alors l'ouvert peut être quoi ? s'il était possible de définir des faisceaux sur un espace topologique muni d'une topologie de fermés, ça aurais été agréable que U par exemple soit une sous variété algébrique, donc les sections sont une sortes de polynômes sur des sous variétés algébriques. Alors, est ce qu'il est possible de construire ce faisceau ? Est ce qu'il existe déjà en géométrie algébrique ce genre de notion un faisceau de polynômes sur des fermés de Zariski, en particulier, des sous variétés algébriques ?

Merci d'avance. :happy3:

[mathelot]

bonjour barbu23,

peux tu rappeler ce qu'est un faisceau au sens de Grothendieck ? aurais tu des exemples concrêts pour nous éclairer ?

merci.

[barbu23]

Un faisceau est un préfaisceau qui vérifie les conditions de recollement.
Comme exemple de faisceau sur un espace topologique , je propose : avec : : faisceau de fonctions constants à valeurs dans .

[L.A.]

Quel sens est-ce que tu donnes à " P : U -> C, P \in C[X] " ? U étant un ouvert d'un espace quelconque a priori, c'est difficile de lui appliquer un polynôme.

L'exemple que je t'ai donné, c'est effectivement le faisceau constant (attention, il faut supposer X irréductible sinon ce n'est qu'un préfaisceau, ou définir les sections comme localement constantes égales à des polynômes).

Pour ton problème de fermé, si tu pars d'un schéma (X,O_X) et que tu considères un faisceau d'idéaux I (autrement dit un O_X-module tel que I(U) est un idéal de O_X(U)), alors le faisceau quotient O_X/I (prendre le préfaisceau U -> O_X(U)/I(U) et le compléter en un faisceau) est un faisceau d'anneaux sur X dont le support est un fermé Y (il faut sans doute supposer I quasi-cohérent quelque part). Donc Y est muni d'une structure naturelle de sous-schéma fermé (Y,O_X/I). Réciproquement (à revérifier si je dis pas de bêtises), si Y est un fermé, les sections qui s'annulent sur Y forment un faisceau d'idéaux I, ce qui permet de le munir d'une structure de sous-schéma fermé par quotient.

[barbu23]

Quel sens est-ce que tu donnes à " P : U -> C, P \in C[X] " ? U étant un ouvert d'un espace quelconque a priori, c'est difficile de lui appliquer un polynôme.

Je ne sais pas. C'est ce que je cherche à comprendre. Comment définit -t-on souvent une fonction continue sur un espace topologique quelconque : ? C'est à dire, quel sens donne-t-on à , c'est difficile aussi d'appliquer à , non ? Je ne me suis jamais posé cette question avant. Parce qu'on a l'habitude de travailler dans un ouvert d'un Banach ou Hilbert au plus, qui sont des espaces plat. Si est un espace topologique quelconque, il se peut que X ait une courbure non nulle, donc, comme les variétés ( sphère, tore, ... etc ) qui ont une courbure constante.

L'exemple que je t'ai donné, c'est effectivement le faisceau constant (attention, il faut supposer X irréductible sinon ce n'est qu'un préfaisceau, ou définir les sections comme localement constantes égales à des polynômes).

Peux tu stp, me rappeler la définition d'un faisceau localement constant, par exemple le faisceau ou . est ce que, c'est

Pour ton problème de fermé, si tu pars d'un schéma (X,O_X) et que tu considères un faisceau d'idéaux I (autrement dit un O_X-module tel que I(U) est un idéal de O_X(U)), alors le faisceau quotient O_X/I (prendre le préfaisceau U -> O_X(U)/I(U) et le compléter en un faisceau) est un faisceau d'anneaux sur X dont le support est un fermé Y (il faut sans doute supposer I quasi-cohérent quelque part). Donc Y est muni d'une structure naturelle de sous-schéma fermé (Y,O_X/I). Réciproquement (à revérifier si je dis pas de bêtises), si Y est un fermé, les sections qui s'annulent sur Y forment un faisceau d'idéaux I, ce qui permet de le munir d'une structure de sous-schéma fermé par quotient.

Merci beaucoup, je voulais dire, est ce qu'on peux définir un faisceau sur un espace topologique avec est la topologie des fermés de Zariski ( ou même n'importe quelle topologie de fermés de ) tel que : espace des sections sur un fermé ou fermé de Zariski de .

Merci d'avance.

[barbu23]

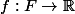Si est fermé, la section ne serait tout simplement pas différentiable sur la frontière, et donc, on ne peut pas lui appliquer l'opérateur de bord pour obtenir 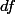. C'est pour cette raison là il me semble qu'on ne définit pas un faisceau sur X muni d'une topologie de fermés, non ?
Et il y'a encore un point qui me gène est qu'on définit des applications régulières ou rationnelles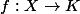 ou 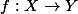sur des variétés algébriques qui sont des fermés ( et sont des variétés algébriques ), et donc, il est possible de définir des sections d'un faisceau sur des fermés, non ?

[barbu23]

Bonjour à tous,

Pourquoi parle -t-on toujours de faisceaux dont les sections sont des fonctions continues, ou différentiables ou holomorphes, ou méromorphes ... etc, mais, jamais on n'entend parler de faisceaux dont les sections sont des polynômes ?

Merci d'avance.

[L.A.]

Tout dépend du contexte, si tu es en géométrie analytique complexe, les sections seront des fonction holomorphes ou méromorphes, si tu es en géométrie algébrique, les sections seront des polynômes (sections globales de Spec K[X_1,...,X_n]) ou des fractions rationnelles (localisation).

Ca me fait penser qu'on ne parle peut-être pas tout à fait de la même chose depuis le début... d'où l'utilité d'être plus précis sur ce que tu cherches...

[barbu23]

les sections seront des polynômes (sections globales de Spec K[X_1,...,X_n]) ou des fractions rationnelles (localisation).

Ca me fait penser qu'on ne parle peut-être pas tout à fait de la même chose depuis le début... d'où l'utilité d'être plus précis sur ce que tu cherches...

Merci tu as tout dit. :happy3:
Je vais voir ça en détail seul. Je pense pouvoir me débrouiller seul dans la suite. Seulement, il y'a un passage que je ne comprends pas bien :

... les sections seront des polynômes (sections globales de Spec K[X_1,...,X_n]) ou des fractions rationnelles (localisation).

- Pourquoi les polynômes ne peuvent ps être des sections locales, contrairement au fractions rationnelles ?
- Je ne comprends pas la place de la localisation dans cette histoire là, peux tu détailler un peu plus stp pour voir plus claire le lien qui existe entre la localisation est les sections locales représentés par les fractions rationnelles ?
- Pourquoi parles tu de schémas et tu préfères ne pas parler tout simplement de variétés algébriques ? Moi, je m'intéresse un petit peu à la conjecture de Hodge ( tu connais certes de quoi il s'agit ), c'est pourquoi, je préfères utiliser les variétés algébriques au lieu des schémas. Est ce qu'il est plutôt judicieux de travailler dans le cadre des schémas pour étudier la conjecture de Hodge mieux que les variétés algébriques surtout lorsqu'il s'agit de groupes de chow ? Bref, je cherche à trouver une correspondance entre les groupe de chow et les espaces de cohomologies d'une résolution d'un faisceau dont les sections sont des polynômes. Pour le moment, je viens juste d'apprendre qu'il existe une cohomologie pour les variétés algébriques, et même pour les schémas, mais, je n'ai aucune idée de quoi il s'agit, c'est encore floue pour moi tout ça.

Voilà une bref histoire de ce que je cherche avec précision. J'espère que j'ai répondu à ton interrogation. J'espère que tu peux m'aider maintenant. :happy3:

Merci d'avance. :happy3:

[L.A.]

Je parle de schémas parce que j'ai appris la géométrie algébrique (il n'y a pas si longtemps) à partir des schémas. Pour moi les variétés algébriques sont des schémas intègres, séparés et de type fini sur un corps algébriquement clos.

Les sections locales peuvent être des polynômes... si elles sont des restrictions de sections globales. Sur X = Spec A avec A = K[X_1,...,X_n] intègre, les sections globales sont O_X(X) = A et le corps des fonctions (qui rassemble toutes les sections, globales ou pas) est Frac(A) = K(X_1,...,X_n). Les sections définies en un point p (idéal premier) sont les éléments du localisé O_{X,p} = A_p inclus dans Frac(A).

Conjecture de Hodge ou groupes de Chow, non, je ne connais pas... (je devrais, peut être...)

[barbu23]

Bonsoir : :happy3:

Les sections locales peuvent être des polynômes... si elles sont des restrictions de sections globales. Sur X = Spec A avec A = K[X_1,...,X_n] intègre, les sections globales sont O_X(X) = A et le corps des fonctions (qui rassemble toutes les sections, globales ou pas) est Frac(A) = K(X_1,...,X_n).

Merci beaucoup pour ta réponse. :happy3:
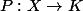- Tu affirmes que est l'espace des sections globales, donc : un polynôme : est définie par : avec : 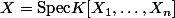, mais, j'ai du mal à comprendre comment on peut évaluer un polynôme par un idéal premier de . Il faut que je révise mes leçons, je sais. :ptdr: Je ne maîtrise pas bien la théorie des schémas. :happy3:
- Pourquoi appelles tu corps des fonctions, et tu t'abstiens de l'appeler corps des fractions de polynômes au lieu de cette appellation que tu choisisses ? On se restreint à 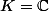, pour simplifier le problème. A vrai dire, les autres cas ne m’intéressent pas.

Les sections définies en un point p (idéal premier) sont les éléments du localisé O_{X,p} = A_p inclus dans Frac(A)

Peux tu m'expliquer ta phrase çi-dessus ?
l'anneau des sections locales s'écrit : , mais qu'est ce que ça veut dire une section définie en un point ? cela voudrait-il dire qu'il est défini uniquement en un point 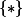tel que 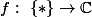, ou bien elle est même définie au voisinage de ?
Et excuse moi pour ces questions qui peuvent te sembler stupide, mais sont très importants pour moi. :happy3:

Merci infiniment. :happy3:

Edit :

Pour moi les variétés algébriques sont des schémas intègres, séparés et de type fini sur un corps algébriquement clos

Est ce que tout schéma intègre, séparé, et de type fini sur un corps algébriquement clos ( par exemple : ) n'est en réalité qu'une variété algébrique ?

Merci d'avance. :happy3:

[L.A.]

- Du point de vue des schémas, évaluer une section en un point où elle est définie 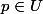correspond à regarder cette section dans le corps résiduel . Du point de vue des variétés, on ne garde que les points rationnels d'un schéma X sur un corps K, c'est à dire les points p pour lesquels k(p) = K (k(p) étant naturellement une extension de K par X -> Spec K).

Donc, du point de vue des variétés, P définit bien une fonction de U (ou U(K)) dans K ; du point de vue des schémas, on rajoute des points génériques (un pour chaque fermé irréductible de la variété) et cette évaluation arrive dans des extensions de K.

- Le corps des fonctions d'un schéma intègre (son anneau local en le point générique) est aussi le corps de fractions de tout ouvert affine.

- Je voulais dire "section définie sur un voisinage de p" plutôt que "section définie en p". Ca revient au même puisque les sections sont définies sur des ouverts.

[barbu23]

Merci beaucoup. Je ne sais pas comment te remercier, grâce à toi, je commence à saisir l'idée pour laquelle la théorie des schémas a été conçu. ça me donne vraiment envie de recommencer à étudier la théorie des schémas à nouveau. La première fois que j'ai découvert les schémas, j'avoue, je n'ai rien compris, et maintenant, grâce à cette discussion, plusieurs choses commencent à s'élucider dans mon esprit, merci beaucoup. :happy3:

[barbu23]

Est ce que tu peux m'expliquer la manière qui permet de visualiser de manière simple l'objet 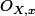: l'anneau des germes au point 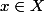. Je réussis facilement à comprendre de quoi est fait , mais pas, 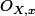, j'ai envie d'écrire : anneau des sections défini en un unique point, parce que, dans certains ouvrages, surtout anglais : , et cette égalité pour moi, veut dire qu'une section sur signifie qu'elle est définit en chaque point de , c'est à dire : 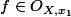et 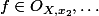avec : 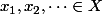, c'est à dire : 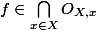, est ce que c'est vrai ça ?
Je sais que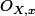 est l'anneau des germes en , c'est à dire l'espace quotient : définie par la relation d'équivalence :
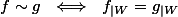avec 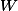un voisinage de ouvert de , mais cette définition est ambiguë pour moi car elle ne me permet pas de voir le lien qui existe entre et 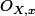. J'aimerai pouvoir réussir à comprendre pourquoi 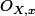a été conçu, et le voir un jour très simplifié, parce que la structure de 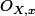est trop compliquée : ensemble des classes d'équivalence qui contient plusieurs fonctions égales au voisinage de , ça me dit rien. :triste: :help:

Merci d'avance pour ton aide. :happy3:

[mathelot]

Bonjour L.A,

aurais tu un cours à ce propos ?

merci.

[barbu23]

Je sais que est l'anneau des germes en , c'est à dire l'espace quotient : définie par la relation d'équivalence :
avec un voisinage de ouvert de , mais cette définition est ambiguë pour moi car elle ne me permet pas de voir le lien qui existe entre et . J'aimerai pouvoir réussir à comprendre pourquoi a été conçu, et le voir un jour très simplifié, parce que la structure de est trop compliquée : ensemble des classes d'équivalence qui contient plusieurs fonctions égales au voisinage de , ça me dit rien.

Pour être plus clair sur ce que je voulais dire par ce paragraphe dans la citation çi dessus, est qu'il est complètement incommode de voir un fibre : comme l'espace quotient par la relation d'équivalence dans la citation çi - dessus, car l'authentique définition d'un fibre est , et on sait théoriquement que la limite inductive d'un système inductive quelconque est définie à isomorphisme près, c'est à dire : si est un système inductif et sa limite inductive, alors avec définie "par construction", c'est à dire fabriqué aléatoirement parmi une infinité de possibilités ( comme c'est le cas de çi dessus ) ne reflète pas réellement la nature de l'objet ( i.e : car d'un coté le lien entre et est un isomorphisme qui n'est ni une immersion ni un plongement l'un dans l'autre, donc et ne sont pas identiques mais différents, mais leurs éléments agissent de la même manière entre eux seulement ) en plus, par la relation d'équivalence que vous connaissez certainement, n'est qu'un exemple parmi plusieurs à isomorphisme près qui peut jouer le rôle de limite inductive des . Bref, ce que je cherches à vous dire est qu'il n'est pas commode de visualiser un fibre par la méthode de "construction" d'un représentant de la classe d'isomorphisme à , mais chercher à comprendre la nature de cette limite inductive à partir de son lien avec , c'est pourquoi, j'ai dit est ce que ? Donc, finalement, comment je peux visualiser à partir de ? Est ce que, c'est comme j'ai dit ci-dessus ? c'est à dire : ?

Merci d'avance. :happy3:

[Ben314]

Salut,
Juste une petite remarque : je n'y connait absolument que dalle en "faisceaux", mais vu la définition que tu donne du fibré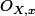 avec ton quotient de , j'ai un tout petit peu l'impression que pour que ait du sens, y'aurais comme qui dirait intérêt à ce que 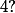soit un ouvert.
Donc tes , je pense que ça risque pas d'avoir beaucoup de sens, et si par hasard ça en as un, ça m'étonnerais profondément que ça ait quelque chose à voir avec 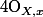qui, par définition, dépend de ce qui se passe au voisinage de 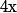et pas uniquement de ce qui se passe au point .

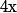C'est un peu comme si tu voulais définir la dérivée f'(xo) en un point xo en ne connaissant que la valeur de f(xo) : ça risque pas de suffire...

[barbu23]

Bonsoir @Ben314,

Salut,
Juste une petite remarque : je n'y connait absolument que dalle en "faisceaux", mais vu la définition que tu donne du fibré avec ton quotient de , j'ai un tout petit peu l'impression que pour que ait du sens, y'aurais comme qui dirait intérêt à ce que soit un ouvert.

C'est écrit aussi là : http://math.stackexchange.com/questions/946369/understanding-the-mechanics-of-gluing-sections-of-presheaves-to-obtain-sheaves , vers le bas.

Donc tes , je pense que ça risque pas d'avoir beaucoup de sens, et si par hasard ça en as un, ça m'étonnerais profondément que ça ait quelque chose à voir avec qui, par définition, dépend de ce qui se passe au voisinage de et pas uniquement de ce qui se passe au point .

Non, la seul définition qu'il y'a du fibre est par sa limite inductive, et il n'y'a pas une définition du fibré en qui dépend de ce qui se passe au voisinage de , c'est juste une "construction" par isomorphisme, parmi tant de constructions possibles, c'est ce que j'ai expliqué dans mon message précédent. :happy3: