DM terminale S, suite et fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 10:51
par shaunarbt » 19 Oct 2014, 10:51
titine a écrit:f(n+1) est la dérivée de f(n) par l'énoncé.
On te dit que f(1) , f(2) , .... sont les dérivées successives de f.
Tu veux démontrer par récurrence que f(n) est de la forme (x² +anx +bn)e^x
Pour cela tu supposes que c'est vrai pour f(n).
Tu calcules f(n+1) = (f(n))'
Tu dois alors avoir f(n+1) qui est de la forme (x² + a(n+1)x + b(n+1))e^x
Pour la question 1b) à la fin de mon hérédité je trouve:f(n+1)=(x^2+a(n+1)(x)+b(n+1)(x)xe^x
= (x^2+(an+2)(x)+(an+bn))e^X
(d'apres l'énoncé de la question 2.)ou alors, je n'ai pas le droit de me servir de la suite de l'énoncé et je conclue juste en disant
f(n+1)=(x^2+a(n+1)(x)+b(n+1)(x)xe^x
=f'(x)
= e^x(x^2+3x+2) (d'après la dérivé de la question 1a)
Et je conclue en disant que pour tout entier n, on a f(n)=(x^2+a(n)(x)+b(n)(x))e^x
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 10:54
par titine » 19 Oct 2014, 10:54
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 11:08
par shaunarbt » 19 Oct 2014, 11:08

Voici la question 2 b) et c)
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 11:34
par titine » 19 Oct 2014, 11:34
shaunarbt a écrit:Pour la question 1b) à la fin de mon hérédité je trouve:
f(n+1)=(x^2+a(n+1)(x)+b(n+1)(x)xe^x
= (x^2+(an+2)(x)+(an+bn))e^X (d'apres l'énoncé de la question 2.)
ou alors, je n'ai pas le droit de me servir de la suite de l'énoncé et je conclue juste en disant
f(n+1)=(x^2+a(n+1)(x)+b(n+1)(x)xe^x
=f'(x)
= e^x(x^2+3x+2) (d'après la dérivé de la question 1a)
Et je conclue en disant que pour tout entier n, on a f(n)=(x^2+a(n)(x)+b(n)(x))e^x
Tu supposes que f(n) (x) = (x² + a(n)x + b(n)) e^x
Tu dérives et eu trouves :
f(n+1) (x) = (f(n))' (x) = (x² + (a(n) + 2)x + (a(n) + b(n))) e^x
Donc f(n+1) (x) est bien de la forme (x² + a(n+1)x + b(n+1)) e^x
avec a(n+1) = a(n) + 2 et b(n+1) = a(n) + b(n)
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 11:42
par shaunarbt » 19 Oct 2014, 11:42
Très bien. Je comprend. Pour la récurrence je me sers essentiellement de l'énoncé, et de la dérivé de f(x). Maintenant pour la question 2) b et c, comment puis je faire, je ne comprend pas ce symbole de "somme"
-
mathelot
 par mathelot » 19 Oct 2014, 13:06
par mathelot » 19 Oct 2014, 13:06
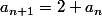
on calcule

(c'est du cours, suite arithmétique de raison r=2)
 (1)
(1)on somme les égalités (1) de k=0 à (n-1) , soit n égalités en tout
la somme des termes

est téléscopique et se simplifie en

-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 13:52
par titine » 19 Oct 2014, 13:52
As tu compris l'explication de mathelot ?
On a b(n+1) = a(n) + b(n)
Donc :
b(2) = a(1) + b(1)
b(3) = a(2) + b(2)
b(4) = a(3) + b(3)
......................
b(n) = a(n-1) + b(n-1)
En additionnant membre à membre toutes ces égalités :
b(2)+b(3)+b(4)+...+b(n) = a(1)+a(2)+a(3)+...+a(n-1) + b(1)+b(2)+b(3)+...+b(n-1)
En simplifiant il reste :
b(n) = a(1)+a(2)+a(3)+...+a(n-1) + b(1)
Or b(1) = 2 donc on a bien :
b(n) = a(1)+a(2)+a(3)+...+a(n-1) + 2
Pour l'expression de b(n) :
On sait calculer a(1)+a(2)+a(3)+...+a(n-1) (somme des termes d'une suite arithmétique.
Donc on en déduit b(n)
Pour c) :
il suffit de calculer a(2013) et b(2013) avec les expressions trouvées et on a f(2013)
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 17:21
par shaunarbt » 19 Oct 2014, 17:21
Je ne vois pas comment calculer ces termes pour en déduire l'expression de bn.
a1=3 ; a2=5 ; a3= 7 ect.. Mais je ne vois pas quoi faire d'autre pour en déduire bn..
B(n+1)= b(n) + (a(n)+2) ?
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 17:22
par shaunarbt » 19 Oct 2014, 17:22
Par ailleurs, je ne comprend pas l'explication de mathelot.
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 17:41
par titine » 19 Oct 2014, 17:41
As tu compris ceci :
titine a écrit:On a b(n+1) = a(n) + b(n)
Donc :
b(2) = a(1) + b(1)
b(3) = a(2) + b(2)
b(4) = a(3) + b(3)
......................
b(n) = a(n-1) + b(n-1)
En additionnant membre à membre toutes ces égalités :
b(2)+b(3)+b(4)+...+b(n) = a(1)+a(2)+a(3)+...+a(n-1) + b(1)+b(2)+b(3)+...+b(n-1)
En simplifiant il reste :
b(n) = a(1)+a(2)+a(3)+...+a(n-1) + b(1)
Or b(1) = 2 donc on a bien :
b(n) = a(1)+a(2)+a(3)+...+a(n-1) + 2
?
Ensuite, pour exprimer b(n) :
b(n) = a(1)+a(2)+...+a(n-1) + 2
On commence par calculer a(1)+a(2)+a(3)+...+a(n-1) (somme des termes d'une suite arithmétique.
Si tu ne te rappelles pas la formule tu peux la trouver par exemple :
ici
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 17:43
par shaunarbt » 19 Oct 2014, 17:43
Je sais d'apres mon cours de premiere que la somme de n termes consécutifs d'une suite arithmétique est égale à la demi-somme des premier et dernier termes, multipliée par le nombre de termes. Mais je n'ai jamais utilisé cette formule du coup je ne vois pas comment l'utiliser.
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 17:55
par shaunarbt » 19 Oct 2014, 17:55
Oui pour la démonstration j'ai compris ce que je n'arrive pas à faire c'est trouver l'expresson de bn. D'apés la formule Sn=n(2+Un)/2 ? Comment cela m'aide à trouver Bn?
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 18:20
par titine » 19 Oct 2014, 18:20
shaunarbt a écrit:Je sais d'apres mon cours de premiere que la somme de n termes consécutifs d'une suite arithmétique est égale à la demi-somme des premier et dernier termes, multipliée par le nombre de termes. Mais je n'ai jamais utilisé cette formule du coup je ne vois pas comment l'utiliser.
C'est ça, donc :
(an) étant une suite arithmétique,
a(1) + a(2) + ... + a(n-1) = (1er terme + dernier terme) * nombre de termes /2
= (a(1) + a(n-1))*(n-1)/2
(en effet de a(1) à a(n-1) il y a (n-1) termes)
Ça va ?
Or a(1) = 3
Et on a vu que a(n) = 1 + 2n donc a(n-1) = 1 + 2(n-1) = 2n- 1
Donc a(1) + a(2) + ... + a(n-1) = ...
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 18:31
par shaunarbt » 19 Oct 2014, 18:31
Sn=(3+2n-1)*(n-1)/2 ?
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 18:39
par titine » 19 Oct 2014, 18:39
shaunarbt a écrit:Sn=(3+2n-1)*(n-1)/2 ?
Oui et donc comme b(n) = Sn + 2 ....
As tu bien compris tout ce que je t'ai expliqué ?
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 19:03
par shaunarbt » 19 Oct 2014, 19:03
Oui mais pourquoi Bn= Sn + 2 ?
C'est parce que b1=2 ?
Après je met au même dénominateur ? Ou je laisse Sn + 2 ?
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 19:41
par titine » 19 Oct 2014, 19:41
On a vu que :
titine a écrit:On a b(n+1) = a(n) + b(n)
Donc :
b(2) = a(1) + b(1)
b(3) = a(2) + b(2)
b(4) = a(3) + b(3)
......................
b(n) = a(n-1) + b(n-1)
En additionnant membre à membre toutes ces égalités :
b(2)+b(3)+b(4)+...+b(n) = a(1)+a(2)+a(3)+...+a(n-1) + b(1)+b(2)+b(3)+...+b(n-1)
En simplifiant il reste :
b(n) = a(1)+a(2)+a(3)+...+a(n-1) + b(1)
Or b(1) = 2 donc on a bien :
b(n) = a(1)+a(2)+a(3)+...+a(n-1) + 2
Donc b(n) = (3+2n-1)*(n-1)/2 + 2 = (2+2n)(n-1)/2 + 2 = 2(n+1)(n-1)/2 + 2
= (n+1)(n-1) + 2 = n² - 1 + 2 = n² + 1
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 19:50
par shaunarbt » 19 Oct 2014, 19:50
Je vois. Donc on a b(n)= n^2+1 et a(n)= 1+2n
Ainsi pour f(2014), je cherche b(2014)= 2014^2+1 et a(2014)= 1+2x2014
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 19 Oct 2014, 20:11
par titine » 19 Oct 2014, 20:11
shaunarbt a écrit:Je vois. Donc on a b(n)= n^2+1 et a(n)= 1+2n
Ainsi pour f(2014), je cherche b(2014)= 2014^2+1 et a(2014)= 1+2x2014
Oui, c'est ça.
-
shaunarbt
- Membre Naturel
- Messages: 29
- Enregistré le: 18 Oct 2014, 10:04
-
 par shaunarbt » 19 Oct 2014, 20:55
par shaunarbt » 19 Oct 2014, 20:55
Je fais la somme de a(2014)+b(2014) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités

