Analyse combinatoire : binôme de newton
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Bropamda304
- Messages: 9
- Enregistré le: 05 Oct 2014, 22:52
-
 par Bropamda304 » 05 Oct 2014, 23:12
par Bropamda304 » 05 Oct 2014, 23:12
Bonjour à tous,
Je suis nouveau sur le forum.
Mon soucis: déterminer le nombre de terme qu'il y a dans
^n)
. Je sais qu'il faut développer par le binôme de newton sur la forme
+c)^n)
mais arrivé à ça je bloque. De plus je sais que le résultat sera

"combinaison de n dans n+2" mais je ne vois comment y arriver.
Une piste ou la résolution me ferait grand plaisir. Merci;)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 06 Oct 2014, 07:13
par fatal_error » 06 Oct 2014, 07:13
salut,
pour la formule exacte, tu peux voir
http://en.wikipedia.org/wiki/Multinomial_theoremmaintenant si ton but c'est juste de compter le nombre de termes, ben c'est viteuf..
(a+b)^n => n+1 termes
^n)
on pose
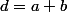
^n = \bigsum_{k=0}^n a_k d^kc^{n-k})
avec

les combinaisons

ca sert à rien non plus
^n \eq \bigsum_{k=0}^n d^k)
or

donne k+1 termes...
donc tu sommes
k+1 pour k=0 à n
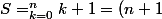+ \frac{n(n+1)}{2})
la vie est une fête


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Oct 2014, 08:00
par chan79 » 06 Oct 2014, 08:00
salut
les termes de
^n)
sont de la forme

avec u+v+w=n
il s'agit donc de trouver le nombre de triplets (u,v,w) de
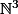
tels que u+v+w=n
c'est donc

Pour
^n)
ce serait

On utilise:
Le nombre de p-uplets
)
de

tels que

est


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Oct 2014, 09:52
par Ben314 » 06 Oct 2014, 09:52
Et, pour ceux qui veulent "aller plus loin", dans le développement de
^n)
, le coefficient qu'il y a devant un terme de la forme

(avec

) est

qui est noté

et est appelé "coefficient multinational" :
^n\ =\ \ \sum_{n_1+n_2+...+n_d=n}\frac{n!}{n_1!n_2!...n_d!}a_1^{n_1}a_2^{n_2}...a_d^{n_d})
Dans le cas d=2, on retrouve les bien connus "coefficients binomiaux" et la formule du binôme de Newton.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Oct 2014, 09:58
par chan79 » 06 Oct 2014, 09:58
Ben314 a écrit: et est appelé
"coefficient multinational" :
^n\ =\ \ \sum_{n_1+n_2+...+n_d=n}\frac{n!}{n_1!n_2!...n_d!}a_1^{n_1}a_2^{n_2}...a_d^{n_d})
Dans le cas d=2, on retrouve les bien connus "coefficients binomiaux" et la formule du binôme de Newton.
salut
coefficient multinomial, plutôt :zen:
-
Bropamda304
- Messages: 9
- Enregistré le: 05 Oct 2014, 22:52
-
 par Bropamda304 » 06 Oct 2014, 10:05
par Bropamda304 » 06 Oct 2014, 10:05
chan79 a écrit:salut
coefficient multinomial, plutôt :zen:
Un grand merci a vous tous!!;);)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités