Lim arctan
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 04 Oct 2014, 14:38
par hazal_kaya » 04 Oct 2014, 14:38
lim (arctanx-x)/x²
x=>0

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Oct 2014, 14:51
par Ben314 » 04 Oct 2014, 14:51
Salut,
-x}{x^2}<br />=\lim_{y\to 0}\frac{y-\tan(y)}{\tan^2(y)}<br />=\lim_{y\to 0}\frac{\cos(y)\big(y\cos(y)-\sin(y)\big)}{\sin^2(y)}=\lim_{y\to 0}\frac{y\cos(y)-\sin(y)}{\sin^2(y)})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 04 Oct 2014, 15:03
par hazal_kaya » 04 Oct 2014, 15:03
y doit etre entre -pi/2 et pi/2 ?
-
mathelot
 par mathelot » 04 Oct 2014, 16:58
par mathelot » 04 Oct 2014, 16:58
salut,
utilise le théorème de L'Hospital . De tête, la limite cherchée est 0

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Oct 2014, 17:02
par chan79 » 04 Oct 2014, 17:02
mathelot a écrit:salut,
utilise le théorème de L'Hospital . De tête, la limite cherchée est 0
c'est pas 0 ? (avec un DL)
-
mathelot
 par mathelot » 04 Oct 2014, 17:05
par mathelot » 04 Oct 2014, 17:05
...................
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 04 Oct 2014, 17:16
par hazal_kaya » 04 Oct 2014, 17:16
Non appart l hôpital y a t il pas d autre methode comme de touver arctanx -x .... entre qqchose et qqchose dont la lim est 0
-
mathelot
 par mathelot » 04 Oct 2014, 17:29
par mathelot » 04 Oct 2014, 17:29
si!
poser
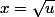
ou
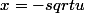
selon les cas x>0 ou x<0
c'est une méthode applicable au programme français
(ni DL ni thm de L'Hospital)
Qu'y a t il dans le programme marocain de Terminale ? vous avez des DL ?
-
mathelot
 par mathelot » 04 Oct 2014, 18:32
par mathelot » 04 Oct 2014, 18:32
hazal_kaya a écrit:lim (arctanx-x)/x²
x=>0
On pose
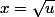
-\sqrt{u}}{u})
où
=arctan(\sqrt{x})-\sqrt{x})
=\frac{1}{2(x+1) \sqrt{x}}-\frac{1}{2 \sqrt{x}}=\frac{- \sqrt{x}}{2(x+1)})
pour
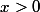
et ensuite, on applique le théorème des accroissements finis.
la fonction g à dériver en x=0+ est continue sur
le fermé [0;1] et dérivable sur l'ouvert ]0,1]
dans ces conditions,
=\lim_{ \rightarrow 0+} \ g')
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 04 Oct 2014, 20:23
par hazal_kaya » 04 Oct 2014, 20:23
Oui merci bien ) :ptdr:
-
mathelot
 par mathelot » 04 Oct 2014, 21:44
par mathelot » 04 Oct 2014, 21:44
bonne soirée :dodo:
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 06 Oct 2014, 11:44
par hazal_kaya » 06 Oct 2014, 11:44
Si on pose x=tanø
lim ( arctan(x) - x)/x =lim (arctan(tanø)-tanø)/tan^2 (ø)
= lim (ø - tanø)/tan^2 (ø)
=lim cosø(øcosø-sinø)/sin^2(ø)
Mais je trouve l'infini !?
Où ai j fait la faute?
-
hazal_kaya
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Oct 2014, 12:55
-
 par hazal_kaya » 08 Oct 2014, 19:35
par hazal_kaya » 08 Oct 2014, 19:35
personne !! :mur:
-
Black Jack
 par Black Jack » 09 Oct 2014, 18:55
par Black Jack » 09 Oct 2014, 18:55
DL de arctan(x) = x - x³/3 + o(x³)
lim(x-->0) [(arctan(x)-x)/x²] = lim(x-->0) [(x - x³/3 -x)/x²] = lim(x-->0) [-x/3] = 0
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
