Calculs de sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 27 Sep 2014, 12:44
par Maths-ForumR » 27 Sep 2014, 12:44
Bonjour,
Comment résoudre :
1) ;) ;) 2^k (pk)
0
2) ;) ;) (k-j)²
1
Merci d'avance !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 27 Sep 2014, 17:43
par Sa Majesté » 27 Sep 2014, 17:43
Salut
Est-ce
1)

2) Là il y a un pb de p et de j
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 27 Sep 2014, 18:18
par Maths-ForumR » 27 Sep 2014, 18:18
Le début oui mais (p k) correspond au coef binomial donc il sont entre ( ) l'un sur l'autre P (en haut) et K (en bas)
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 27 Sep 2014, 18:20
par Maths-ForumR » 27 Sep 2014, 18:20
Pour le 2) c'est
Somme (k=1 à n) de la somme (j=1 à 2n) de (k-j)²
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 27 Sep 2014, 23:06
par deltab » 27 Sep 2014, 23:06
Bonsoir
Maths-ForumR a écrit:Pour le 2) c'est
Somme (k=1 à n) de la somme (j=1 à 2n) de (k-j)²
Pour la 1) \sum_{} \sum_{}{p \choose k) 2^k
développes (1+a)^p. Qu'ontienr t'on pour a=2}
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 27 Sep 2014, 23:31
par deltab » 27 Sep 2014, 23:31
Bonsoir
Maths-ForumR a écrit:Pour le 2) c'est
Somme (k=1 à n) de la somme (j=1 à 2n) de (k-j)²
Pour la 1)

développes
^p)
. Qu'obtient'on pour
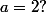
Tu doit retrouver

Pour la 2) c'est bien
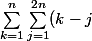^2)
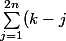^2= \sum_{j=1}^{n}(k-j)^2+\sum_{j=n+1}^{2n}(k-j)^2)
Fais un changement d'indices dans
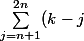^2)
pour te ramener à une somme de 1 à n. Après quelques calculs fastidieux avec des changements d'indices, tu seras amené à calculer

Pour indication tu devras trouver
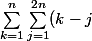^2=\dfrac{4n^4-n^2}{3})
PS: Tu pourra démontrer par récurrence que
(2p+1)}{6})
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 28 Sep 2014, 10:28
par Maths-ForumR » 28 Sep 2014, 10:28
(1+2)^p = 1^k x 2^(p-k) = 2^(p-k) ?
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 28 Sep 2014, 13:48
par Mikihisa » 28 Sep 2014, 13:48
Utilise la formule du binôme de newton (a+b)^n = ?
Lorsque a=1 on obtient somme(0 à n) C(n,k)b^k
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 28 Sep 2014, 14:22
par deltab » 28 Sep 2014, 14:22
Maths-ForumR a écrit:(1+2)^p = 1^k x 2^(p-k) = 2^(p-k) ?
Je t'ai demandé de développer
^p)
(donc formule du binôme de Newton),
^p=\sum_{k=0}^p \cdots\cdots)
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 02 Oct 2014, 22:24
par Maths-ForumR » 02 Oct 2014, 22:24
J'ai réussi a faire la 1er somme mais je n'arrive vraiment pas a la 2ème quelqu'un peut -il me détailler le calcule svp ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 03 Oct 2014, 02:07
par deltab » 03 Oct 2014, 02:07
Bonjour
Maths-ForumR a écrit:J'ai réussi a faire la 1er somme mais je n'arrive vraiment pas a la 2ème quelqu'un peut -il me détailler le calcule svp ?
Te détailler le calcul, pas question . Qu'as tu fait pour 2)
En développant
^2)
, on aura
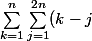^2=\sum_{k=1}^n \sum_{j=1}^{2n}k^2+\sum_{k=1}^n\sum_{j=1}^{2n} j^2 - 2\sum_{k=1}^n \sum_{j=1}^{2n} jk)
.
Continues
PS.
La méthode que j'ai donnée auparavant est plus longue que celle-la. Dans les 2 cas on a besoin de

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités