Bonjour, je suis nouveau dur le forum et je ne sais pas comment on met mes symboles mathématiques donc je mets une photo en attendat de savoir le faire (désolé)
Je dois trouver les critères de divisibilités par 2 et 5, par 11 et 13, si quelqu'un pouvait m'expliquer ce serait gentil car je ne voit pas comment demontrer que a=10q+r ?
Merci d'avance :we:
Divisibilité
13 messages
- Page 1 sur 1
bonsoir,
la division euclidienne correspond à un partage équitable.
par exemple, ssi tu veux diviser 131 par 6,
tu donnes 1 à chacun (1)
ça diminue la quantité à diviser de 6.
Il y a encore 131-6 = 125 à répartir.
on continue (1) jusqu'à l'arrêt.
Il reste alors une quantité non divisée, qui est le reste r
avec
dans le cas général, on écrit a=bq+r avec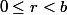
la division euclidienne correspond à un partage équitable.
par exemple, ssi tu veux diviser 131 par 6,
tu donnes 1 à chacun (1)
ça diminue la quantité à diviser de 6.
Il y a encore 131-6 = 125 à répartir.
on continue (1) jusqu'à l'arrêt.
Il reste alors une quantité non divisée, qui est le reste r
avec
dans le cas général, on écrit a=bq+r avec
Soch a écrit:Je viens ici pour avoir de l'aide pas pour me faire rabaisser.. J'ai compris ce qu'il fallait faire c'est juste que j'ai du mal a trouver comment on le démontre, est-ce qu'il faut remplacer par des nombres ?
démontrer c'est simplement écrire la division euclidienne par 10 par définition de la division euclidienne ...
je te concède que tu aies du mal à saisir que cela suffise ... (écrire une définition est une preuve)
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
modulo 7


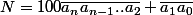
Soit un nombre entier.
un nombre entier.
soit m son nombre de centaines et r le nombre formé avec ses deux derniers chiffres
N est divisible par 7 si et seulement si 2m+r est divisible par 7
N=123456 est divisible par 7 ssi 2468+56=2524 est divisible par 7
ssi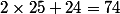 est divisible par 7
est divisible par 7
donc non, le reste de la division de N=123456 par 7 vaut 4.
etc..
zut, ce n'est pas ce que demande l'exercice mais bon, "mon" critère tient la route.
modulo 7






Soit N un entier
soit m son nombre de millions et r le nombre formé de ses six derniers chiffres
N est divisible par 7 si et seulement si m+r est divisible par 7
Soit
soit m son nombre de centaines et r le nombre formé avec ses deux derniers chiffres
N est divisible par 7 si et seulement si 2m+r est divisible par 7
N=123456 est divisible par 7 ssi 2468+56=2524 est divisible par 7
ssi
donc non, le reste de la division de N=123456 par 7 vaut 4.
etc..
zut, ce n'est pas ce que demande l'exercice mais bon, "mon" critère tient la route.
modulo 7
Soit N un entier
soit m son nombre de millions et r le nombre formé de ses six derniers chiffres
N est divisible par 7 si et seulement si m+r est divisible par 7
Merci pour vos reponses, pour rédiger pour le 1 je dis que a=10q+u c'est resoudre la division euclidienne de a par 10 ? je ne vois pas comment rédiger en fait :( ? Et comme on sait que a congru a u modulo deux et que a congru a u modulo 5 car 10 divise 2 et divise 5 ou que 10=2*5 ? Je ne vois pas la non plus comment rédiger ?
Soch a écrit:Merci pour vos reponses, pour rédiger pour le 1 je dis que a=10q+u c'est resoudre la division euclidienne de a par 10 ? je ne vois pas comment rédiger en fait? Et comme on sait que a congru a u modulo deux et que a congru a u modulo 5 car 10 divise 2 et divise 5 ou que 10=2*5 ? Je ne vois pas la non plus comment rédiger ?
il n'y a rien à rédiger ... juste à écrire
a = 10q + r = 2(5q) + r = 5(2q) + r
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
