Sous-groupe engendré / morphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Oct 2014, 19:18
par capitaine nuggets » 01 Oct 2014, 19:18
Bonsoir,
Je bloque sur l'exercice suivant :
On se donne un morphisme de groupes
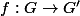
et un sous-ensemble

de

. On me demande de comparer
)
et

.
J'ai conjecturer que
=)
mais je n'arrive pas à le prouver.
Auriez-vous une idée ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 01 Oct 2014, 20:15
par cuati » 01 Oct 2014, 20:15
Bonsoir,
par double inclusion :

donc
\subset f())
, or ce dernier est un sous groupe de G', donc
)
.
Réciproquement :
Soit
)
, il existe alors
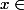
tel que
=y)
.
Or, par définition du groupe engendré

, il existe
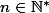
,
\in E^n)
et
\in\{-1;1\}^n)
tels que :

. Donc du fait que

est un morphisme :
=f(x_1)^{\alpha_1}.\dots.f(x_n)^{\alpha_n} \in)
.
Donc
\subset)
.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Oct 2014, 20:20
par capitaine nuggets » 01 Oct 2014, 20:20
Salut !
Ok, mais je ne comprends pas ce passage :
cuati a écrit:(...), or ce dernier est un sous groupe de G', donc
)
.
De qui parles-tu ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 01 Oct 2014, 20:26
par jlb » 01 Oct 2014, 20:26
Double-inclusion?
E C donc f(E) C f() ....
soit y dans f() donc il existe x dans tel que y=f(x) . Comme x est dans , il existe un nb fini d'éléments a1,a2,a3..., de E ou inverses d'éléments de E tq x=a1a2a3... et après tu utilises la propriété de morphisme de f pour montrer que y apprtient à
à vérifier comme d'habitude
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 01 Oct 2014, 20:30
par cuati » 01 Oct 2014, 20:30
On a :
\subset f(<E>))
.
Or,

est un sous-groupe de

donc
)
est un sous groupe de
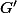
. (Car l'image d'un groupe par un morphisme est un groupe).
Pour résumer :
\subset f())
, donc
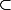>)
mais comme
)
est un groupe, on a
>=f())
.
Donc
)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Oct 2014, 20:39
par capitaine nuggets » 01 Oct 2014, 20:39
cuati a écrit:On a :
\subset f(<E>))
.
Or,

est un sous-groupe de

donc
)
est un sous groupe de
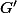
. (Car l'image d'un groupe par un morphisme est un groupe).
Pour résumer :
\subset f())
, donc
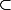>)
mais comme
)
est un groupe, on a
>=f())
.
Donc
)
Merci pour tes explications :++:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Oct 2014, 20:57
par capitaine nuggets » 01 Oct 2014, 20:57
J'aurai une autre question, que se passe-t-il si

est injectif ou surjectif ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Oct 2014, 21:17
par capitaine nuggets » 01 Oct 2014, 21:17
J'aurai une autre question, que se passe-t-il si

est injective ou surjective ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 01 Oct 2014, 21:40
par cuati » 01 Oct 2014, 21:40
capitaine nuggets a écrit:J'aurai une autre question, que se passe-t-il si

est injective ou surjective ?
Question très vague,
On peut dire que

est injective si et seulement si
=\{e\})
ou

est le neutre de

.
Lorsque

est surjective on a une propriété intéressante :
Pour tout sous-groupe
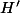
de
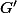
,
)
est un sous-groupe de

.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Oct 2014, 21:48
par Doraki » 01 Oct 2014, 21:48
cuati a écrit:Lorsque

est surjective on a une propriété intéressante :
Pour tout sous-groupe
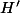
de
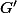
,
)
est un sous-groupe de

.
c'est vrai tout le temps ça, pas besoin d'avoir f surjective.
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 01 Oct 2014, 21:52
par cuati » 01 Oct 2014, 21:52
Oui Doraki, merci de rafraichir ma mémoire qui se fait vieille...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
.
.
est un sous-groupe de
donc
est un sous groupe de
. (Car l'image d'un groupe par un morphisme est un groupe).
, donc
mais comme
est un groupe, on a
.
est injective ou surjective ?