Arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Le Chat
- Membre Relatif
- Messages: 128
- Enregistré le: 19 Nov 2012, 23:11
-
 par Le Chat » 30 Sep 2014, 21:48
par Le Chat » 30 Sep 2014, 21:48
Bonjour,
Je n'arrive pas à résoudre cette exercice ; j'ai essayé par récurrence sur n:
Prouver que
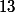
divise
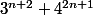
pour tout entier n
Je prouve le cas n=1, supposons le cas n=k
cas n= k+1:
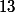
divise
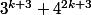
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Sep 2014, 22:00
par Doraki » 30 Sep 2014, 22:00
3^(n+2) + 4^(2n+1) = 9*3^n + 4*16^n
Comme 16 est congru à 3 et que 9 est congru à -4, ....
-
Le Chat
- Membre Relatif
- Messages: 128
- Enregistré le: 19 Nov 2012, 23:11
-
 par Le Chat » 30 Sep 2014, 22:18
par Le Chat » 30 Sep 2014, 22:18
Doraki a écrit:3^(n+2) + 4^(2n+1) = 9*3^n + 4*16^n
Comme 16 est congru à 3 et que 9 est congru à -4, ....
salut,
on n'a pas encore vu les congruences, il y a une autre façon?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Sep 2014, 22:23
par Doraki » 30 Sep 2014, 22:23
!??
Tu peux toujours réécrire 16^n en (13+3)^n puis développer, t'obtiens des tas de multiples de 13, puis un 3^n, que tu regroupes avec l'autre 3^n pour avoir 13*3^n.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Sep 2014, 22:33
par chan79 » 30 Sep 2014, 22:33
Le Chat a écrit:Bonjour,
Je n'arrive pas à résoudre cette exercice ; j'ai essayé par récurrence sur n:
Prouver que
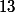
divise
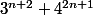
pour tout entier n
donc, on suppose
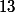
divise
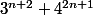
soit

On considère:

Remplace

par

-
Le Chat
- Membre Relatif
- Messages: 128
- Enregistré le: 19 Nov 2012, 23:11
-
 par Le Chat » 30 Sep 2014, 22:43
par Le Chat » 30 Sep 2014, 22:43
Doraki a écrit:!??
Tu peux toujours réécrire 16^n en (13+3)^n puis développer, t'obtiens des tas de multiples de 13, puis un 3^n, que tu regroupes avec l'autre 3^n pour avoir 13*3^n.
merci, c'est fait.
mais il y a plus simple encore, comme on n'a pas encore vu le binôme de newton.
-
Le Chat
- Membre Relatif
- Messages: 128
- Enregistré le: 19 Nov 2012, 23:11
-
 par Le Chat » 30 Sep 2014, 22:58
par Le Chat » 30 Sep 2014, 22:58
chan79 a écrit:donc, on suppose
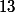
divise
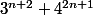
soit

On considère:

Remplace

par


=
<br />= 13m)
avec m entier. :zen:
tiens, j'y avais pas pensé :hum:

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Oct 2014, 15:42
par zygomatique » 01 Oct 2014, 15:42
Le Chat a écrit:Bonjour,
Je n'arrive pas à résoudre cette exercice ; j'ai essayé par récurrence sur n:
Prouver que
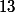
divise
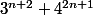
pour tout entier n
Je prouve le cas n=1, supposons le cas n=k
cas n= k+1:
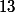
divise
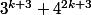
salut

est multiple de 13
première méthode ::
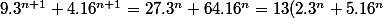 + 3^n - 16^n)
et on conclut connaissant l'identité remarquable

deuxième méthode
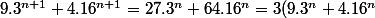 + 52.16^n = 3(9.3^n + 4.16^n) + 13.4.16^n)
et on conclut avec l'hypothèse (de récurrence)
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
LA solution
- Membre Relatif
- Messages: 165
- Enregistré le: 28 Déc 2012, 17:11
-
 par LA solution » 01 Oct 2014, 17:19
par LA solution » 01 Oct 2014, 17:19
mon frere essaye d applique la congruence mondulo 13 ET le tour est joué

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Oct 2014, 17:26
par zygomatique » 01 Oct 2014, 17:26
LA solution a écrit:mon frere essaye d applique la congruence mondulo 13 ET le tour est joué
as-tu lu ce qui précède .... :mur:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
divise
pour tout entier n
divise