Dm sur les Suites à moitié compris

[jeune]

Bonjour à tous , je suis en classe de première S , j'ai touhjours eu de très bon résultats mais la je suis perdue , j'ai un Dm à faire pour dans 4 jours j'ai commencer voici le lien : http://www.ac-grenoble.fr/lycee/vincent.indy/IMG/pdf_act_suites.pdf attention les traits après d0 c'est un = et pareille pour en dessous . Je dois faire l'activité 2 et 3 , pour l'activité 2 j' n'ai pas compris la question 1 , pour la question 2 : j'ai déterminer d1 , d2 et d3 =
d1 = f(d0)=;)1+(3)²=;)10=3.16
d2= f(d1)=;)1+(3.16)²=3.31
d3= f(d2)=;)1+(3.31)²=3.46 j'ai également répondue à la question 3 : Non car il s'agit d'un suite definie par recurrence , ul faudrait don calculer tous les termes qui precedent d2011. et aussi à la question 4: d'après la calculatrice :U20= 5.3852 . j'aurais donc besoins de votre aide pour la premiere question , je ferais l'activité 3 moi même dans quelques jours . Merci d'avance :help:

[mathelot]

bonjour,

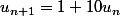
les suites sont des séquences, des listes, des énumérations de nombres.


exemple:
1 11 111 1111 11111 111111 1111111 11111111

On numérote ces nombres en débutant à l'indice 0



on devine que le 6ème nombre a l'indice 5 et comporte six "1"

ici, il y a une formule de récurrence, pour passer d'un nombre u(n) au suivant d'indice (n+1)
,noté u(n+1), il suffit de multiplier par 10 et d'ajouter 1

on écrit ça

[jeune]

re , merci pour cet indication , mais en fait , je ne comprends pas vraiment la question : Montrer que
dn+1= ;)1+dn² , je pense qu'il y a un rapport avec la figure si on m'aurais demander de trouver dn+1 par rapport a dn la je pense pourvoir le faire mais la on me donne dn+1 enfin bref je suis perplexe :mur: , aussi j'ai realiser l'activité 3 si vous pourriez me dire si cela vous parraît correcte ou si je doit rectifier :


1)pour Un=2n²-3 calculer:

Un+1= 2(n+1)²-3
= 2(n²+2n+1)-3
=2n²+4n+2-3
2n²+4n-1

Un-1=2(n-1)²-3
= 2(n²+2n+1)-3
=2n²+4n+2-3
=2n²+4n-1

U2n=2(2n)²-3
=4n²-3

U2n+1=2(2n+1)²-3
=2(2n²+2n+1)-3
=4n²+4n+2-3
=4n²+4n-1

2) pour Vn=3^n calculer:

Vn+1=3^(n+1)
=3n+3

Vn+2 = 3^(n+2)
=3n+6

V2n= 3^(2n)
=6n
Merci bien :we:

[mathelot]

: Montrer que
dn+1= 1+dn² , je pense qu'il y a un rapport avec la figure

dn+1 est la longueur de la nouvelle hypotènuse (dn étant l'ancienne hypotènuse)

1)pour Un=2n²-3 calculer:

Un+1= 2(n+1)²-3
= 2(n²+2n+1)-3
=2n²+4n+2-3
2n²+4n-1

Un-1=2(n-1)²-3
= 2(n²+2n+1)-3
=2n²+4n+2-3
=2n²+4n-1

U2n=2(2n)²-3
=4n²-3

U2n+1=2(2n+1)²-3
=2(2n²+2n+1)-3
=4n²+4n+2-3
=4n²+4n-1

2) pour Vn=3^n calculer:

Vn+1=3^(n+1)
=3n+3 non

Vn+2 = 3^(n+2)
=3n+6 non

V2n= 3^(2n) =9^n
=6n
Merci bien :we:

............

[jeune]

Un-1=2(n-1)²-3
= 2(n²-2n+1)-3
=2n²-4n+2-3
=2n²-4n-1

U2n=2(2n)²-3
=8n²-3

Vn+1=3^(n+1)
=3^n

Vn+2 = 3^(n+2)
= 9^n

V2n= 3^(2n)
=6^n

[mathelot]

aurais tu le temps de lire du cours ( intitulé "les puissances") ? tout est expliqué.

[chan79]

[jeune]

Merci pour votre site très complet j'ai du français à faire mais dés que j'ai terminer je lis et corrige mes erreurs merci beaucoup

[mathelot]

merci pour vos encouragements. A+

[jeune]

Alors pour Vn+1=3^n+1
=3^1n

Vn+2=3^n+2
=3^2n

V2n=3^2n
=3^2n

[jeune]

j'ai compris mais je ne voit pas trop ou vous voulez en venir , ils s'agit de quel question svp .

Quelqu'un pour m'aidez pour la premiere question svp

[chan79]

j'ai compris mais je ne voit pas trop ou vous voulez en venir , ils s'agit de quel question svp .

c'est l'activité 2

[jeune]

[quote="chan79"] oui merci , j'ai terminer ce dp mais je n'arrive pas à répondre a la question : Conjecturer l'expression de dn en fonction de n ; il faut dire si lasuite est croissante ou décroissant ?

[mathelot]

oui........

de plus

quelle est la nature de la suite dont les termes sont ?

[jeune]

Alors fait , conjecturer dn en fonction de n c'est trouver une relation qui les lie ; (j'ai vue cela dans mon cahier de cour ) entre chaque therme , on ajoute 0.15 mais la je doit trouver une expression sans n+1 mais uniquement avec n mais je n'arrive pas a trouver de raisonnement