Fonction dérivé n fois
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 17:41
par Dwarfs43 » 24 Sep 2014, 17:41
Bonjour
Je suis bloqué sur un exercice sans savoir même comment commencer :
legende :
= compris
^(x)=juste pour dire que c'est à la position de la puissance, mais c'est pour dire "dérivé x fois"
Soit f:x |-> cos(2x)
Montrer que pour tout n N* et tout x R
f^(n) (n) = 2^n cos(2x+(npi)/2)
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 17:42
par Bimbooo » 24 Sep 2014, 17:42
et pourquoi pas une récurrence ?
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 17:44
par Dwarfs43 » 24 Sep 2014, 17:44
J'y ai pensé, mais j'avoue ne pas du tout réussir l'hérédité, il faudrait me guider ;x
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 17:48
par Bimbooo » 24 Sep 2014, 17:48
ok, donc l'initialisation est faite ?
C'est quoi la dérivée (n+1)ème d'une fonction ? (en fonction de la dérivée nième)
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 17:54
par Dwarfs43 » 24 Sep 2014, 17:54
C'est la dérivé n elle même dérivé ?
donc f^(n)'
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 18:00
par Bimbooo » 24 Sep 2014, 18:00
Exactement, alors par récurrence on veut montrer pour tout
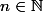
)
: pour tt

de

} (x) = 2^n cos(2x+n\frac{\pi}{2}))
. Qu'est-ce qui te bloque ?
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 18:04
par Dwarfs43 » 24 Sep 2014, 18:04
Il y a plusieurs trucs que je comprends pas, déjà à quoi nous sert "f:x -> cos(2x)" et la démarche à faire pour l'hérédité ...
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 18:09
par Bimbooo » 24 Sep 2014, 18:09
bah f c'est la fonction au départ, tu la dérives n fois et tu veux savoir ce que ça donne.
Ensuite le raisonnement pour l'hérédité est toujours le même : tu supposes P(n) et tu montres P(n+1).
Je t'ai donné P(n), qu'est-ce que c'est P(n+1) ? Comment le prouver ?
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 18:13
par Dwarfs43 » 24 Sep 2014, 18:13
Ok c'est déjà plus clair, pour le prouver je fais
P(n)'=P(n+1)
tu fais comment pour écrire de manière mathématique, se serai plus simple pour moi
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 18:18
par Bimbooo » 24 Sep 2014, 18:18
En fait P(n) c'est la propriété "pour tt x bla bla bla".
Tu peux pas dériver ça ! Mais tu supposes P(n) c'est à dire, tu dis :
Supposons que pour tt

,
}(x) = 2^n cos(x + n\frac{\pi}{2}))
Et après tu veux déduire P(n+1), tu peux me dire ce qu'est la propriété P(n+1) ?
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 18:29
par Dwarfs43 » 24 Sep 2014, 18:29
Bin je dois prouver que
la dérivé de :
 2^{n+1} cos(2x+({n+1})\frac{\pi}{2}))
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 18:35
par Bimbooo » 24 Sep 2014, 18:35
Dwarfs43 a écrit:Bin je dois prouver que
la dérivé de :
 2^{n+1} cos(x+n+1\frac{\pi}{2}))
attention à l'utilisation de ce genre de symbole, ça ne veut rien dire...
Mais je crois que tu as quand même compris, tu sais dériver une composée ? (attention aux parenthèses dans le cos)
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 18:43
par Dwarfs43 » 24 Sep 2014, 18:43
il me semble, sa donne

(est-ce qu'il faut dériver dans le cos ?)
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 18:51
par Bimbooo » 24 Sep 2014, 18:51
excuse moi, j'ai oublié le 2 devant le x précédemment, et tu as du coup fait pareil
C'est une fonction dont x est la variable, n est une constante, 2 puissance n aussi...
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 19:04
par Dwarfs43 » 24 Sep 2014, 19:04
Donc il faut que je prouve que
 = 2^{n+1} cos(2x+({n+1})\frac{\pi}{2}))
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 19:16
par Bimbooo » 24 Sep 2014, 19:16
non ! La dérivée est fausse : tu dérives en fonction de x, pas de n !
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 19:21
par Dwarfs43 » 24 Sep 2014, 19:21
je dois re dans 30minutes environ, j'essaie de faire vite
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 19:56
par Dwarfs43 » 24 Sep 2014, 19:56
Voilà je suis de retour, et j'ai pas compris mon erreur, il faut bien que je dérive
)
-
Bimbooo
- Membre Naturel
- Messages: 31
- Enregistré le: 01 Aoû 2014, 18:40
-
 par Bimbooo » 24 Sep 2014, 20:20
par Bimbooo » 24 Sep 2014, 20:20
Dwarfs43 a écrit:Voilà je suis de retour, et j'ai pas compris mon erreur, il faut bien que je dérive
)
Si f est définie par :
 = 2^n)
, quelle est la dérivée de f ?
-
Dwarfs43
- Membre Naturel
- Messages: 61
- Enregistré le: 10 Sep 2014, 13:08
-
 par Dwarfs43 » 24 Sep 2014, 20:27
par Dwarfs43 » 24 Sep 2014, 20:27
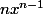
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 109 invités
