DM de mathématiques suite et recurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Queviso86
- Messages: 4
- Enregistré le: 24 Sep 2014, 11:39
-
 par Queviso86 » 24 Sep 2014, 16:11
par Queviso86 » 24 Sep 2014, 16:11
Bonjour je suis bloqué pour deux exercices pouvez vous m'aider ?
1) on souhaite comparer les croissances pour n entier naturel des progressions 3^n et n!.
n u(n)=3^n V(n)= n!
0. 1. 1
1. 3. 1
2. 9. 2
3. 27. 6
4. 81. 24
5. 243. 120
6. 729. 720
A) conjecturer alors une relations d ordre entre u(n) etv (n)
Pour n entier de plus en plus grand.
B) démontrer la. Conjecture a l aide d un raisonnement par récurrence.
2) démontrez pour tout n appartenant a N*, que :
a^n - b^n = (a-b) ( somme i=0 et n-1) a^(n-1-i) * b^i
Aide : a^(n+1) - b^(n+1) = a* a^n -b * b^n
-
mathelot
 par mathelot » 24 Sep 2014, 16:15
par mathelot » 24 Sep 2014, 16:15
Bonjour,
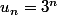
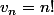
Ecris les relations de récurrence vérifiées par
chaque suite, indépendemment de l'autre suite.
tu vas tout de suite deviner laquelle l'emporte
-
Queviso86
- Messages: 4
- Enregistré le: 24 Sep 2014, 11:39
-
 par Queviso86 » 24 Sep 2014, 16:18
par Queviso86 » 24 Sep 2014, 16:18
mathelot a écrit:Bonjour,
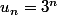
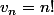
Ecris les relations de récurrence vérifiées par
chaque suite, indépendemment de l'autre.
tu vas tout de suite deviner laquelle l'emporte
Comment ça ?
-
mathelot
 par mathelot » 24 Sep 2014, 16:19
par mathelot » 24 Sep 2014, 16:19
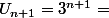
!=)
ce qui est demandé est une formule de récurrence.
-
Queviso86
- Messages: 4
- Enregistré le: 24 Sep 2014, 11:39
-
 par Queviso86 » 24 Sep 2014, 16:21
par Queviso86 » 24 Sep 2014, 16:21
ok pour celle la je pensais pas que juste cela était suffisant. mais le reste je suis bloquée.
-
mathelot
 par mathelot » 24 Sep 2014, 16:23
par mathelot » 24 Sep 2014, 16:23
Est ce que tu peux écrire une f
ormule de récurrence pour la suite
)
sachant que

?
qu'est ce qu'une formule de récurrence ?
-
mathelot
 par mathelot » 24 Sep 2014, 16:29
par mathelot » 24 Sep 2014, 16:29
ce que je demandais:
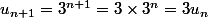
et
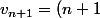!= (n+1) \times n!= (n+1)v_n)
que devines tu ? (= conjecturer)
-
mathelot
 par mathelot » 24 Sep 2014, 16:34
par mathelot » 24 Sep 2014, 16:34
tu peux me donner un retour, svp ?
-
mathelot
 par mathelot » 24 Sep 2014, 16:43
par mathelot » 24 Sep 2014, 16:43
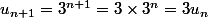
et
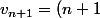!= (n+1) \times n!= (n+1)v_n)
en fait,(v_n) croit beaucoup plus rapidement que (u_n).
ça ne se devine pas sur les premiers termes que tu as écrits
-
mathelot
 par mathelot » 24 Sep 2014, 16:45
par mathelot » 24 Sep 2014, 16:45
tu peux me donner un retour, svp ? j'ai essayé de t'expliquer des aspects intéressants de cet énoncé.
-
mathelot
 par mathelot » 24 Sep 2014, 17:05
par mathelot » 24 Sep 2014, 17:05
l'hypothèse de récurrence à poser est:
P(n) := n! > 3^n
Elle récurre dès

par modus ponens.
Elle ne
s'initialise qu'au bout d'un certain nombre d'itérations, à
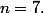
au début, elle est fausse.
modus ponens:

___________

-
mathelot
 par mathelot » 24 Sep 2014, 17:23
par mathelot » 24 Sep 2014, 17:23
 := n! > 3^n) (1)
(1) (2)
(2)! > 3^{n+1})
par produit de (1) et (2).
Elle est donc héréditaire dès n=2 par modus ponens (ie, via une certaine façon de démontrer
qui est de poser l'hypothèse de récurrence)
Elle est vraie à partir de n=7
(en fait elle est héréditaire dès le début car elle est fausse pour n <7)
-
Queviso86
- Messages: 4
- Enregistré le: 24 Sep 2014, 11:39
-
 par Queviso86 » 24 Sep 2014, 19:01
par Queviso86 » 24 Sep 2014, 19:01
Merci beaucoup c'est trés gentil :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
