DM suites et récurrence avec fonction

par **kiloalove** » 21 Sep 2014, 13:38

bonjour, j'ai ce devoir à rendre mais je bloque sur une question et mes recherches sont sans succès

f(x)=x+(1/2)

-(1/3)

u

=1/2 et pour tout entier naturel n,

=f(

)=

+(1/2)

-(1/3)

je dois d'abord etudier le sens de variation de f puis démontrer par récurrence que pour tout entier naturle n, 1/2

u

3/2

c'est là que je ne sais pas comment m'y prendre
merci de m'aider, cela serait très aimable à vous :lol3:

par **kiloalove** » 21 Sep 2014, 14:11

help please :/

par **kiloalove** » 21 Sep 2014, 15:26

up ! ça fait deux heures que je ne trouve pas

par **mathelot** » 21 Sep 2014, 15:42

bonjour,

montre que f conserve l'intervalle et étudie sa monotonie.

Si elle est croissante , alors l'inégalité

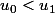
est héréditaire

par **kiloalove** » 21 Sep 2014, 15:48

bonjour, merci de votre réponse
mais que signifie f conserve l'intervalle ?
elle n'est pas monotone

par **kiloalove** » 21 Sep 2014, 15:49

Veuillez cliquer sur une des icônes de « Réponse rapide » dans les messages ci-dessus pour activer la réponse rapide.

par **mathelot** » 21 Sep 2014, 15:50

par **kiloalove** » 21 Sep 2014, 17:12

mathelot a écrit:

je comprends cette réflexion mais je ne vois pas du tout comment m'en servir et comment la rédiger :/

par **mathelot** » 21 Sep 2014, 17:33

On remplace

par

par **kiloalove** » 21 Sep 2014, 17:40

mathelot a écrit:On remplace par

donc on commence la récurrence avec x avant de remplacer par un ? je ne vois pas du tout comment débuter la récurrence en fait...

par **mathelot** » 21 Sep 2014, 18:07

Le terme suivant

, c'est

,ie,

quand on a un terme, on en prend l'image par f, on obtient le terme suivant

par **kiloalove** » 21 Sep 2014, 18:47

ie ?
merci beaucoup pour votre précieuse aide, j'ai compris ça mais je ne vois même pas comment rédiger l'initialisation

par **mathelot** » 21 Sep 2014, 21:11

si f est croissante dans l'intervalle

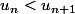
se démontre par récurrence

par **kiloalove** » 21 Sep 2014, 21:27

ah d'accord merci
et pour 1/2 et 3/2 de chaque côté, je fais comment ?

par **mathelot** » 21 Sep 2014, 21:33

c'est indépendant ; on peut récurrer sur les deux propriétés indépendemment car

par **kiloalove** » 21 Sep 2014, 22:10

donc concrètement je récurre sur quoi ?

par **mathelot** » 21 Sep 2014, 22:14

une fois sur

c'était une difficulté supplémentaire qui tient à la façon d'écrire l'énoncé

par **kiloalove** » 21 Sep 2014, 22:51

ah d'accord je comprends mieux, merci à vous de m'avoir répondu, je vous recontacte si je rencontre un problème
bonne soirée :)

par **Bimbooo** » 21 Sep 2014, 23:12

Pas besoin de récurrence pour

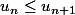
, comme on a étudié f, on peut voir que

est positif sur

, car si on a montré que

est dans cet intervalle pour tout n,

l'est aussi.

par **kiloalove** » 22 Sep 2014, 22:24

je comprends mieux, merci beaucoup à vous deux !!