Problème d'analyse

[adamNIDO]

Bonjour,


j'ai passé un concours de mathématiques hier, elle était dure pour moi



Franchement j'ai rien fait dans ce problème


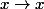
1) comme la fonction est continue sur donc elle est continue sur donc la fonction est continue par somme et produit de fonctions continues sur Ainsi s(x) est bien définie sur

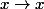
2) comme la fonction est dérivable sur donc elle est dérivable sur donc la fonction est dérivable par somme et produit de fonctions dérivable sur Ainsi s(x) est de classe sur

3) soit
je pense pour montrer que on doit passer par l’intégrale puisque est de classe sur

[Bimbooo]

Attention, n'est pas la fonction qui à associe , mais qui associe la série de terme général . Il s'agit pour montrer que est bien définie de prouver l'existence et la convergence de cette série pour

Attention au fait, il ne faut pas oublier de dire : comme quotient de fonctions continues dont le dénominateur ne s'annule pas pour justifier la continuité comme tu le faisais

[alm]

lL lui manque donc de justifier la convergence de la série en question.
Suggestion:
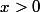
Pour , on a la convergence absolue puisque et il est connu que la série numérique est convergente (de somme )

[mathelot]

c'est la convergence normale (en particulier, sur tout compact de R+*, elle donne la convergence et la continuité de la somme, sauf erreur)

[adamNIDO]

Attention, n'est pas la fonction qui à associe , mais qui associe la série de terme général . Il s'agit pour montrer que est bien définie de prouver l'existence et la convergence de cette série pour

Attention au fait, il ne faut pas oublier de dire : comme quotient de fonctions continues dont le dénominateur ne s'annule pas pour justifier la continuité comme tu le faisais

Bonjour,

Donc etudier la fonction revient à étudie la suite

oui j'ai oublie de dire "dont le dénominateur ne s'annule pas"

[adamNIDO]

lL lui manque donc de justifier la convergence de la série en question.
Suggestion:
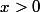
Pour , on a la convergence absolue puisque et il est connu que la série numérique est convergente (de somme )

Bonjour,


oui, merci pour votre suggestion .

[adamNIDO]

c'est la convergence normale (en particulier, sur tout compact de R+*, elle donne la convergence et la continuité de la somme, sauf erreur)

Bonjour,

merci donc pour la solution de la question 1 je vais dire ce que tu as dis ou bien je peux prendre la suggestion de alm .

[deltab]

Bonjour

Bonjour,
merci donc pour la solution de la question 1 je vais dire ce que tu as dis ou bien je peux prendre la suggestion de alm .

1) Je peux dire les deux. Matelot a parlé de la convergence normale qui n'est que la conséquence de ce qu'a écrit Alm sauf qu'il faut isoler le terme d'indice qui lui n'est borné sur , . Il fallait étudier la série et on a bien la convergence normale de cette série sur ( je dis bien fermé en )
2) Idem: Étudies la dérivabilité de la série
3) Fais un changement d'indices dans S(x+1).

[adamNIDO]

Bonjour

1) Je peux dire les deux. Matelot a parlé de la convergence normale qui n'est que la conséquence de ce qu'a écrit Alm sauf qu'il faut isoler le terme d'indice qui lui n'est borné sur , . Il fallait étudier la série et on a bien la convergence normale de cette série sur ( je dis bien fermé en )
2) Idem: Étudies la dérivabilité de la série
3) Fais un changement d'indices dans S(x+1).

merci beaucoup monsieur, je vais vérifier ça après car maintenant je me suis concentré sur autre chose
je porte a votre connaissance que j'ai trouvé la solution de ce problème dans le site de Monsieur david Delaunay