Devoir sur les vecteurs (seconde )
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 20 Sep 2014, 12:45
par Shew » 20 Sep 2014, 12:45
cinthyasnape a écrit:Donc pour résumer la question 1,on a fait ceci
BG + (-CA +CB)-AG
-AC+CB=AC+CB
AC+CB=AB
-AG=-(GA)=GA
GA+AB=GB
BG+GB=-GB+GB=0
pour la question 2
démontrer que BI+CB-GI=CG
vous me dites de "transformez le vecteur GI en fonction de GC"
oui CI...+..i=GI,heu..j'ai toujours pas compris
mon professeur de math m'a dit "d'insérer le point G (en utilisant Chasles) dans chacun des vecteurs de gauche et la simplification s'opère tout de suite pour trouver le vecteur CG" mais j'ai pas comprit Je ne comprend vraiment rien....
En passer par le point G oui mais c'est tellement plus simple de transformer
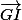
cela permet de retrouver l'egalité recherchée en deux coups .
Je vous ai demandé de transformer le vecteur
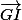
en fonction de
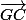
et je vous ai donné comme indice
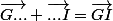
donc de toute evidence vous avez au départ
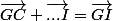
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 20 Sep 2014, 19:45
par cinthyasnape » 20 Sep 2014, 19:45
Shew a écrit:En passer par le point G oui mais c'est tellement plus simple de transformer
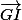
cela permet de retrouver l'egalité recherchée en deux coups .
Je vous ai demandé de transformer le vecteur
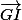
en fonction de
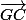
et je vous ai donné comme indice
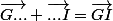
donc de toute evidence vous avez au départ
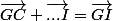
Donc heu GC+BI ?=GC ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 20 Sep 2014, 19:48
par Shew » 20 Sep 2014, 19:48
cinthyasnape a écrit:Donc heu GC+BI ?=GC ?
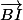
??? Cela vous semble t'il correspondre à Chasles ?
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 10:49
par cinthyasnape » 21 Sep 2014, 10:49
Shew a écrit: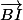
??? Cela vous semble t'il correspondre à Chasles ?
Heu..
GC+CI=GI ,,??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 13:05
par Shew » 21 Sep 2014, 13:05
cinthyasnape a écrit:Heu..
GC+CI=GI ,,??
Oui c'est ca . Maintenant donnez les vecteurs opposés de
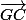
et
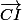
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 13:11
par cinthyasnape » 21 Sep 2014, 13:11
Shew a écrit:Oui c'est ca . Maintenant donnez les vecteurs opposés de
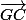
et
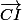
CG et IC ??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 16:01
par Shew » 21 Sep 2014, 16:01
cinthyasnape a écrit:CG et IC ??
Bien!!!!! Maintenant exprimez
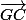
et
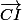
en fonction de leur vecteur opposé respectif (ATTENTION au signe !!!!!)
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 18:36
par cinthyasnape » 21 Sep 2014, 18:36
Shew a écrit:Bien!!!!! Maintenant exprimez
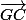
et
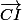
en fonction de leur vecteur opposé respectif (ATTENTION au signe !!!!!)
IC +IG = GC non ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 18:49
par Shew » 21 Sep 2014, 18:49
cinthyasnape a écrit:IC +IG = GC non ?
Non,
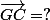
,
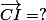
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 18:56
par cinthyasnape » 21 Sep 2014, 18:56
Shew a écrit:Non,
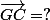
,
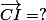
GC=-CI=-GI??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 19:03
par Shew » 21 Sep 2014, 19:03
cinthyasnape a écrit:GC=-CI=-GI??
:hein: :hein: :hein:
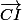
serait il le vecteur opposé de
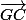
????
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 19:23
par cinthyasnape » 21 Sep 2014, 19:23
Shew a écrit::hein: :hein: :hein:
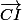
serait il le vecteur opposé de
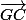
????
non ,le vecteur opposé de GC c'est CG
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 20:04
par Shew » 21 Sep 2014, 20:04
cinthyasnape a écrit:non ,le vecteur opposé de GC c'est CG
Donc ecrivez
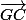
en fonction de
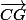
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 20:16
par cinthyasnape » 21 Sep 2014, 20:16
Shew a écrit:Donc ecrivez
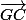
en fonction de
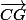
GC en fonction de CG:
CG +IC =GC ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 20:17
par Shew » 21 Sep 2014, 20:17
cinthyasnape a écrit:GC en fonction de CG:
CG +IC =GC ?
Ce n'est pas le sens de la question on l'a fait plusieurs fois ça

Même raisonnement pour
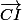
.
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 20:19
par cinthyasnape » 21 Sep 2014, 20:19
Shew a écrit:Ce n'est pas le sens de la question on l'a fait plusieurs fois ça

Même raisonnement pour
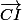
.
donc CI=-IC ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 20:32
par Shew » 21 Sep 2014, 20:32
cinthyasnape a écrit:donc CI=-IC ?
Voilaa!!! De plus d'après la question on a

donc
)
d'après la règle des signes qu'avons nous pour
)
et
)
???
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 20:42
par cinthyasnape » 21 Sep 2014, 20:42
Shew a écrit:Voilaa!!! De plus d'après la question on a

donc
)
d'après la règle des signes qu'avons nous pour
)
et
)
???
heu je ne vois pas ..
mais du coup pour
GC= IC=
je ne voi pas comment compléter
-
cinthyasnape
- Membre Naturel
- Messages: 39
- Enregistré le: 15 Sep 2014, 11:52
-
 par cinthyasnape » 21 Sep 2014, 20:44
par cinthyasnape » 21 Sep 2014, 20:44
cinthyasnape a écrit:heu je ne vois pas ..
mais du coup pour
GC= IC=
je ne voi pas comment compléter
et en plus c'est pour demain..
je suis très loin de finir
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 21 Sep 2014, 20:49
par Shew » 21 Sep 2014, 20:49
cinthyasnape a écrit:heu je ne vois pas ..
mais du coup pour
GC= IC=
je ne voi pas comment compléter
Pourquoi cette egalité ? Ce n'est pas le sens de ma question il s'agit d'appliquer une simple règle des signes .
 = \vec{CG})
et
 = \vec{IC})
. Maintenant qu'on a divisé

, donnez moi le vecteur opposé de
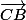
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
