Identification

[echizen]

Bonsoir,

J'essaye de résoudre cet exercice dont les questions sont liés, mais j'ai beau cherché je reste bloqué...

Pour n € N^étoile

1) Trouver trois réels a, b et c tels que pour tout k de N^étoile


J'ai mis sur le même dénominateur et j'essaye de procéder par identification j'obtiens k^2(a+b+c)+k(3a+2b+c)+2(a+b+1/2)=1
Malheureusement je bloque à cette étape.

Je vous remercie

[chan79]

Salut
tu dois résoudre
a+b+c=0
3a+2b+c=0
2a=1

[echizen]

Salut
tu dois résoudre
a+b+c=0
3a+2b+c=0
2a=1

Merci pour votre réponse j'ai trouvé a=c=1/2 et b=-1. Je dois maintenant cancluler la limite de quand n tend vers +infini. Je dirai spontanément qu'il faut étudier la limite du dernier terme qui donne 1/infini donc limite est 0 mais comment pouvons nous la démontrer ?

[chan79]

Cherche des simplifications selon les diagonales montantes

Résultat 1/4

[echizen]

Cherche des simplifications selon les diagonales montantes

Résultat 1/4

Merci pour votre réponse mais je ne comprends pas ce que vous voulez dire par diagonales montantes ?

[deltab]

Bonsoir

Merci pour votre réponse mais je ne comprends pas ce que vous voulez dire par diagonales montantes ?

Si tu écris , ne peux-tu pas écrire la suite des sommes partielles comme une somme télescopique, regardes bien (dans les yeux si je puis me permettre) les deux termes mis entre parenthèses du dernier membre des égalités écrites ci-dessus.
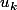
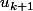
Pour les colonnes montantes, il s'agit de montantes de la gauche vers la droite, les termes écrits sont , et . Corriges l'écriture de

[zygomatique]

Cherche des simplifications selon les diagonales montantes

Résultat 1/4

salut

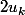
il peut être intéressant car plus visuel de factoriser par 1/2 (ou de multiplier par 2) et de regarder ce qui se passe en écrivant les premiers termes .... pour k = 1, 2, 3, ....