Exercice de fonction

[shashou83]

Vous voulez dire

Oui j'ai eu beaucoup de mal à l'écrire

[shashou83]

Oui j'ai eu beaucoup de mal à l'écrire

Lorsque je fais mon calcul j'obtiens donc racine de (x(carré -2x (carré) + x(carré) + (-x(carré) -8x -x(carré) -7/2) au carré mais (xcarré) au carré sa donne quoi ?

[Shew]

Lorsque je fais mon calcul j'obtiens donc racine de (x(carré -2x (carré) + x(carré) + (-x(carré) -8x -x(carré) -7/2) au carré mais (xcarré) au carré sa donne quoi ?

Non on a ce qui correspond à ce que vous aviez trouvé en calculant f(x) - g(x) .

[shashou83]

Non on a ce qui correspond à ce que vous aviez trouvé en calculant f(x) - g(x) .

Je viens de comprendre mon erreur mais ensuite il ne faut pas la forme canonique pour trouver le maximale ?

[Shew]

Je viens de comprendre mon erreur mais ensuite il ne faut pas la forme canonique pour trouver le maximale ?

Ou cherchez seulement les coordonnées du sommet de la fonction .

[shashou83]

Ou cherchez seulement les coordonnées du sommet de la fonction .

J'ai cherché alpha et beta et j'ai trouvé alpha = -2 et beta = 9/2

[Shew]

J'ai cherché alpha et beta et j'ai trouvé alpha = -2 et beta = 9/2

Utilisez plutot la formule du sommet .

[shashou83]

Quel formule du sommet ?

[Shew]

Quel formule du sommet ?

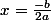
[shashou83]

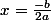
Cest exactement ce que j'ai fais mais au lieu de x j'ai mis alpha

[Sa Majesté]

Pourriez vous m'aidez s'il vous plait j'ai vraiment besoin d'aide je viens de commencé la première S et je n'arrive pas du tout à comprendre mon premier devoir maison je n'ai pas travaillé la dessus au paravent merci de prendre en considération mon message je n'arrive pas à rejoindre une photo des graphique

C'est lequel ton 1er devoir maison ?
Celui-ci ou celui-là ?
http://www.maths-forum.com/exercice-fonction-157683.php

[shashou83]

C'est lequel ton 1er devoir maison ?
Celui-ci ou celui-là ?
http://www.maths-forum.com/exercice-fonction-157683.php

Mon devoir masion est composé de plusieurs exercice